What we think of as time can be seen in an abstract form of a torus. Where the 'now' is at the top, (if the torus was upright like the tire on a car) and the future in front going around the torus to the bottom where it runs into the past. This is not to say that time loops or repeats, it's just an model of how to think about these specific mysteries in quantum physics. Therefore, when a photon goes through the slit and is observed, be it in the interference pattern on the wall or in non interference pattern - when the observation is made, the information travels into the future and resolves with all the other information in the future and continues until it goes around the torus and eventually comes into the past and back to the present moment, while at the same time 'resolving' with other information from the past, up to the present moment. In this way, the outcome is already resolved with the future and the past and the outcome conforms with both. It may be that the changes in the 'now' also makes changes in the future and maybe even changes the past or that it doesn't make changes and it just resolves to be in sync with what the future and the past requires of it. This model can work for the double slit mystery and for entangled particles, including where future actions may influence past events as predicted by physicist Asher Peres in 2000 and realized in a paper reporting the experiment published online April 22 in the journal Nature Physics, led by Xiao-song Ma of the Institute for Quantum Optics and Quantum Information at the University of Vienna.
Question Can time as a torus make sense of quantum physics?
- Thread starter Deon Joubert
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mr Joubert -
I'm not sure if time acts like a torus in the " mystery and for entangled particles, including where future actions may influence past events as predicted by physicist Asher Peres in 2000 and realized in a paper reporting the experiment published online April 22 (2012) in the journal Nature Physics, led by Xiao-song Ma of the Institute for Quantum Optics and Quantum Information at the University of Vienna," which you mention above.
See: "Quantum Theory Needs No Interpretation", Article Published in Physics Today · September 2000, https://www.researchgate.net/publication/2462691
See: "Experimental Delayed-Choice Entanglement Swapping", Published 22 April 2012, https://www.nature.com/articles/nphys2294
However, a view of the apparatus used in 2012 experiment might help in better understanding the experiment in question.
If one views the quantum state as a real physical object, one could get the seemingly paradoxical situation that future actions appear as having an influence on past and already irrevocably recorded events. However, there is never a paradox if the quantum state is viewed as to be no more than a “catalogue of our knowledge” . Then the state is a probability list for all possible measurement outcomes, the relative temporal order of the three observer’s events is irrelevant and no physical interactions whatsoever between these events, especially into the past, are necessary to explain the delayed-choice entanglement swapping. What, however, is important is to relate the lists of Alice, Bob and Victor’s measurement results (see below). On the basis of Victor’s measurement settings and results, Alice and Bob can group their earlier and locally totally random results into subsets which each have a different meaning and interpretation. This formation of subsets is independent of the temporal order of the measurements.
According to the physicist John Wheeler, NeilsBohr said: “No elementary phenomenon is a phenomenon until it is a registered phenomenon.” This should be extended to include: “Some registered phenomena do not have a meaning unless they are put in relationship with other registered phenomena.”
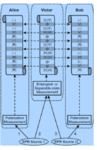


The experimental scheme and the time diagram of the relevant events is shown in Fig. 1 showed that the generation of photons 1 and 2 (event GI) happened at 0 ns (nano-seconds), as the origin of the diagram. The generation of photons 3 and 4 (event GII) happened 1.6 ns later. At 35 ns, the measurements of Alice and Bob (events MA and MB) occurred. The choice of Victor (event CV) was made by the QRNG in the time interval ranging from 49 ns to 348 ns and sent to the tunable BiSA. Due to the fibre delay of photons 2 and 3, at 520 ns Victor performed the bipartite state measurement (event MV) according to the bit value of his choice. Note that our definition of the choice event is very conservative. This is because in addition to the fixed amount of the electrical delay of the EOMs’ driver (45 ns), QRNG (75 ns) and connecting cables (20 ns), we also included 3 times the QRNG autocorrelation time (3⋅10.7 ns ≈ 32 ns) and the on-time of the EOMs (299 ns). This on-time gave the time of event CV a lower bound of 49 ns and an upper bound of 348 ns. As shown in Fig. 1, it is clear to see for each successful run (a 4-fold coincidence count) that not only event MV happened 485 ns later than events MA and MB, but also event CV happened 14 ns to 313 ns later than events MA and MB even in this conservative consideration. Therefore, this configuration unambiguously fulfilled the delayed-choice condition. Note that the main uncertainty of the experiment in time for measurements is the detector jitter, which is about 800 ps.
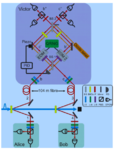
In the entanglement swapping 1-3 procedure, two pairs of entangled photons are produced, and one photon from each pair is sent to Victor. The two other photons from each pair are sent to Alice and Bob, respectively. If Victor projects his two photons onto an entangled state, Alice’s and Bob’s photons are entangled although they have never interacted or shared any common past. What might be considered as even more puzzling is Peres’ idea of “delayed-choice for entanglement swapping” . In this gedanken (thought) experiment, Victor is free to choose either to project his two photons onto an entangled state and thus project Alice’s and Bob’s photons onto an entangled state, or to measure them individually and then project Alice’s and Bob’s photons onto a separable state. If Alice and Bob measure their photons’ polarization states before Victor makes his choice and projects his two photons either onto an entangled state or onto a separable state, it implies that whether their two photons are entangled (showing quantum correlations) or separable (showing classical correlations) can be defined after they have been measured. In order to experimentally realize Peres’ thought experiment, Victor ’s choice and measurement must be placed in the time-like future of Alice’s and Bob’s measurements, providing a “delayed-choice” configuration in any and all reference frames. This is accomplished by (1) proper optical delays for Victor’s photons and (2) a high-speed tunable bipartite state analyzer, which (3) is controlled in real time by a quantum random number generator. Both delay and randomness are needed to avoid the possibility that the photon pairs can “know” in advance which setting will be implemented after they are registered and can behave accordingly by producing results of a definite entangled or a definite separable state. Whether Alice’s and Bob’s photons can be assigned an entangled state or a separable state depends on Victor’s later choice. In Peres’ words: “if we attempt to attribute an objective meaning to the quantum state of a single system, curious paradoxes appear: quantum effects mimic not only instantaneous action-at-a-distance but also, as seen here, influence of future actions on past events, even after these events have been irrevocably recorded.”
Historically, delayed-choice entanglement swapping can be seen as the fascinating consequence of emerging from combining the gedanken* (thought) experiments by Neils Bohr (gedanken, Bohr's term), illustrated by a quantum entanglement double-slit setup, and John Wheeler, illustrated by the complementarity principle, one of the most basic principles of quantum mechanics, with a double-slit apparatus. If both slits are open, the input quantum system exhibits “wave-like” behavior and shows interference on the detector screen. If only one slit is open, the system can only propagate through this slit. In this case, no interference will be observed and the system exhibits “particle-like” behavior with a well-defined path.
In accordance with the complementarity principle, full interference and full path information will never be obtained simultaneously. As an explanation it is often said that any attempt to determine which path a particle takes inside an interferometer disturbs the particle and thus prevents the interference pattern from forming. From a modern point of view, however, interference patterns can arise if and only if no information about the path taken exists either on the particle itself or in the environment, regardless of whether or not an observer accesses this information.
If the choice between complementary experimental settings—one demonstrating interference, one revealing which-path information—is made in the past, an explanation of Bohr’s complementarity can be given in the following way: before the particle enters the interferometer, it “receives” information which setting has been prepared and then behaves correspondingly. For example, the two complementary settings in a photonic Mach-Zehnder configuration can be implemented by inserting or removing the output beam splitter that recombines the two interfering paths. To avoid the possibility that the photon will somehow “know” in advance whether the output beam splitter is chosen to be inserted or not, Wheeler suggested to delay this choice after the photon has passed the input beam splitter.
Many so-called “delayed-choice” experiments have been performed, including the scheme when the choice to insert or remove the output beam splitter is made at a space-time location that is space-like separated from the entrance of the photon in the interferometer According to Wheeler, “we have a strange inversion of the normal order of time. We, now, by moving the mirror in or out have an unavoidable effect on what we have a right to say about the already past history of that photon.” Evidently, even in such a delayed-choice scenario, the choice has to be made in the past light cone of the final detection of the photon.
On the other hand, delayed-choice experiments with entangled photons pave the way for new possibilities, where the choice of measurement settings on the distant photon can be made even after the other photon has been registered. This has been shown in a delayed-choice quantum eraser experiment where the which-path
information of one photon was erased by a later suitable measurement on the other photon. This allowed a posteriori to decide a single-particle characteristic, namely whether the already measured photon behaved as a wave or as a particle. However, while all previous delayed-choice experiments focused on the characteristics of individual particles, delayed-choice entanglement swapping, using a four-partite entangled state, allows, a posteriori, to decide a two-particle characteristic and thus has qualitatively new features. Just as there is a wave-particle duality for single particles, there is an entanglement-separability duality for two particles. Entanglement and separability correspond to two mutually exclusive types of correlations between two particles.
I hope the diagrams of the apparatus used in the 2012 experiments, performed by Xiao-song Ma and his co-authors, and their explanations, as well as an overview of the work of Christopher Fuchs and Asher Perez in their 2000 paper, help to clarify this rather difficult area to grasp. Particle-wave duality, entanglement-separability and delayed choice entanglement are as hard to grasp as the idea of life and death and Schrödinger's cat being in both those states until you open the box the cat is in.
Hartmann352
See: https://arxiv.org/vc/arxiv/papers/1203/1203.4834v1.pdf
* gedanken experiment (German: “thought experiment”) term used by German-born physicist Albert Einstein to describe his unique approach of using conceptual rather than actual experiments in creating the theory of relativity.
For example, Einstein described how at age 16 he watched himself in his mind’s eye as he rode on a light wave and gazed at another light wave moving parallel to his. According to classical physics, Einstein should have seen the second light wave moving at a relative speed of zero. However, Einstein knew that Scottish physicist James Clerk Maxwell’s electromagnetic equations absolutely require that light always move at 3 × 108 metres (186,000 miles) per second in a vacuum. Nothing in the theory allows a light wave to have a speed of zero. Another problem arose as well: if a fixed observer sees light as having a speed of 3 × 108 metres per second, whereas an observer moving at the speed of lightsees light as having a speed of zero, it would mean that the laws of electromagnetism depend on the observer. But in classical mechanics the same laws apply for all observers, and Einstein saw no reason why the electromagnetic laws should not be equally universal. The constancy of the speed of light and the universality of the laws of physics for all observers are cornerstones of special relativity.
See: https://www.britannica.com/science/Gedankenexperiment
I'm not sure if time acts like a torus in the " mystery and for entangled particles, including where future actions may influence past events as predicted by physicist Asher Peres in 2000 and realized in a paper reporting the experiment published online April 22 (2012) in the journal Nature Physics, led by Xiao-song Ma of the Institute for Quantum Optics and Quantum Information at the University of Vienna," which you mention above.
See: "Quantum Theory Needs No Interpretation", Article Published in Physics Today · September 2000, https://www.researchgate.net/publication/2462691
See: "Experimental Delayed-Choice Entanglement Swapping", Published 22 April 2012, https://www.nature.com/articles/nphys2294
However, a view of the apparatus used in 2012 experiment might help in better understanding the experiment in question.
If one views the quantum state as a real physical object, one could get the seemingly paradoxical situation that future actions appear as having an influence on past and already irrevocably recorded events. However, there is never a paradox if the quantum state is viewed as to be no more than a “catalogue of our knowledge” . Then the state is a probability list for all possible measurement outcomes, the relative temporal order of the three observer’s events is irrelevant and no physical interactions whatsoever between these events, especially into the past, are necessary to explain the delayed-choice entanglement swapping. What, however, is important is to relate the lists of Alice, Bob and Victor’s measurement results (see below). On the basis of Victor’s measurement settings and results, Alice and Bob can group their earlier and locally totally random results into subsets which each have a different meaning and interpretation. This formation of subsets is independent of the temporal order of the measurements.
According to the physicist John Wheeler, NeilsBohr said: “No elementary phenomenon is a phenomenon until it is a registered phenomenon.” This should be extended to include: “Some registered phenomena do not have a meaning unless they are put in relationship with other registered phenomena.”



The experimental scheme and the time diagram of the relevant events is shown in Fig. 1 showed that the generation of photons 1 and 2 (event GI) happened at 0 ns (nano-seconds), as the origin of the diagram. The generation of photons 3 and 4 (event GII) happened 1.6 ns later. At 35 ns, the measurements of Alice and Bob (events MA and MB) occurred. The choice of Victor (event CV) was made by the QRNG in the time interval ranging from 49 ns to 348 ns and sent to the tunable BiSA. Due to the fibre delay of photons 2 and 3, at 520 ns Victor performed the bipartite state measurement (event MV) according to the bit value of his choice. Note that our definition of the choice event is very conservative. This is because in addition to the fixed amount of the electrical delay of the EOMs’ driver (45 ns), QRNG (75 ns) and connecting cables (20 ns), we also included 3 times the QRNG autocorrelation time (3⋅10.7 ns ≈ 32 ns) and the on-time of the EOMs (299 ns). This on-time gave the time of event CV a lower bound of 49 ns and an upper bound of 348 ns. As shown in Fig. 1, it is clear to see for each successful run (a 4-fold coincidence count) that not only event MV happened 485 ns later than events MA and MB, but also event CV happened 14 ns to 313 ns later than events MA and MB even in this conservative consideration. Therefore, this configuration unambiguously fulfilled the delayed-choice condition. Note that the main uncertainty of the experiment in time for measurements is the detector jitter, which is about 800 ps.
In the entanglement swapping 1-3 procedure, two pairs of entangled photons are produced, and one photon from each pair is sent to Victor. The two other photons from each pair are sent to Alice and Bob, respectively. If Victor projects his two photons onto an entangled state, Alice’s and Bob’s photons are entangled although they have never interacted or shared any common past. What might be considered as even more puzzling is Peres’ idea of “delayed-choice for entanglement swapping” . In this gedanken (thought) experiment, Victor is free to choose either to project his two photons onto an entangled state and thus project Alice’s and Bob’s photons onto an entangled state, or to measure them individually and then project Alice’s and Bob’s photons onto a separable state. If Alice and Bob measure their photons’ polarization states before Victor makes his choice and projects his two photons either onto an entangled state or onto a separable state, it implies that whether their two photons are entangled (showing quantum correlations) or separable (showing classical correlations) can be defined after they have been measured. In order to experimentally realize Peres’ thought experiment, Victor ’s choice and measurement must be placed in the time-like future of Alice’s and Bob’s measurements, providing a “delayed-choice” configuration in any and all reference frames. This is accomplished by (1) proper optical delays for Victor’s photons and (2) a high-speed tunable bipartite state analyzer, which (3) is controlled in real time by a quantum random number generator. Both delay and randomness are needed to avoid the possibility that the photon pairs can “know” in advance which setting will be implemented after they are registered and can behave accordingly by producing results of a definite entangled or a definite separable state. Whether Alice’s and Bob’s photons can be assigned an entangled state or a separable state depends on Victor’s later choice. In Peres’ words: “if we attempt to attribute an objective meaning to the quantum state of a single system, curious paradoxes appear: quantum effects mimic not only instantaneous action-at-a-distance but also, as seen here, influence of future actions on past events, even after these events have been irrevocably recorded.”
Historically, delayed-choice entanglement swapping can be seen as the fascinating consequence of emerging from combining the gedanken* (thought) experiments by Neils Bohr (gedanken, Bohr's term), illustrated by a quantum entanglement double-slit setup, and John Wheeler, illustrated by the complementarity principle, one of the most basic principles of quantum mechanics, with a double-slit apparatus. If both slits are open, the input quantum system exhibits “wave-like” behavior and shows interference on the detector screen. If only one slit is open, the system can only propagate through this slit. In this case, no interference will be observed and the system exhibits “particle-like” behavior with a well-defined path.
In accordance with the complementarity principle, full interference and full path information will never be obtained simultaneously. As an explanation it is often said that any attempt to determine which path a particle takes inside an interferometer disturbs the particle and thus prevents the interference pattern from forming. From a modern point of view, however, interference patterns can arise if and only if no information about the path taken exists either on the particle itself or in the environment, regardless of whether or not an observer accesses this information.
If the choice between complementary experimental settings—one demonstrating interference, one revealing which-path information—is made in the past, an explanation of Bohr’s complementarity can be given in the following way: before the particle enters the interferometer, it “receives” information which setting has been prepared and then behaves correspondingly. For example, the two complementary settings in a photonic Mach-Zehnder configuration can be implemented by inserting or removing the output beam splitter that recombines the two interfering paths. To avoid the possibility that the photon will somehow “know” in advance whether the output beam splitter is chosen to be inserted or not, Wheeler suggested to delay this choice after the photon has passed the input beam splitter.
Many so-called “delayed-choice” experiments have been performed, including the scheme when the choice to insert or remove the output beam splitter is made at a space-time location that is space-like separated from the entrance of the photon in the interferometer According to Wheeler, “we have a strange inversion of the normal order of time. We, now, by moving the mirror in or out have an unavoidable effect on what we have a right to say about the already past history of that photon.” Evidently, even in such a delayed-choice scenario, the choice has to be made in the past light cone of the final detection of the photon.
On the other hand, delayed-choice experiments with entangled photons pave the way for new possibilities, where the choice of measurement settings on the distant photon can be made even after the other photon has been registered. This has been shown in a delayed-choice quantum eraser experiment where the which-path
information of one photon was erased by a later suitable measurement on the other photon. This allowed a posteriori to decide a single-particle characteristic, namely whether the already measured photon behaved as a wave or as a particle. However, while all previous delayed-choice experiments focused on the characteristics of individual particles, delayed-choice entanglement swapping, using a four-partite entangled state, allows, a posteriori, to decide a two-particle characteristic and thus has qualitatively new features. Just as there is a wave-particle duality for single particles, there is an entanglement-separability duality for two particles. Entanglement and separability correspond to two mutually exclusive types of correlations between two particles.
I hope the diagrams of the apparatus used in the 2012 experiments, performed by Xiao-song Ma and his co-authors, and their explanations, as well as an overview of the work of Christopher Fuchs and Asher Perez in their 2000 paper, help to clarify this rather difficult area to grasp. Particle-wave duality, entanglement-separability and delayed choice entanglement are as hard to grasp as the idea of life and death and Schrödinger's cat being in both those states until you open the box the cat is in.
Hartmann352
See: https://arxiv.org/vc/arxiv/papers/1203/1203.4834v1.pdf
* gedanken experiment (German: “thought experiment”) term used by German-born physicist Albert Einstein to describe his unique approach of using conceptual rather than actual experiments in creating the theory of relativity.
For example, Einstein described how at age 16 he watched himself in his mind’s eye as he rode on a light wave and gazed at another light wave moving parallel to his. According to classical physics, Einstein should have seen the second light wave moving at a relative speed of zero. However, Einstein knew that Scottish physicist James Clerk Maxwell’s electromagnetic equations absolutely require that light always move at 3 × 108 metres (186,000 miles) per second in a vacuum. Nothing in the theory allows a light wave to have a speed of zero. Another problem arose as well: if a fixed observer sees light as having a speed of 3 × 108 metres per second, whereas an observer moving at the speed of lightsees light as having a speed of zero, it would mean that the laws of electromagnetism depend on the observer. But in classical mechanics the same laws apply for all observers, and Einstein saw no reason why the electromagnetic laws should not be equally universal. The constancy of the speed of light and the universality of the laws of physics for all observers are cornerstones of special relativity.
See: https://www.britannica.com/science/Gedankenexperiment
Last edited:
A photon is no more than a way to present light in a less confusing way.What we think of as time can be seen in an abstract form of a torus. Where the 'now' is at the top, (if the torus was upright like the tire on a car) and the future in front going around the torus to the bottom where it runs into the past. This is not to say that time loops or repeats, it's just an model of how to think about these specific mysteries in quantum physics. Therefore, when a photon goes through the slit and is observed, be it in the interference pattern on the wall or in non interference pattern - when the observation is made, the information travels into the future and resolves with all the other information in the future and continues until it goes around the torus and eventually comes into the past and back to the present moment, while at the same time 'resolving' with other information from the past, up to the present moment. In this way, the outcome is already resolved with the future and the past and the outcome conforms with both. It may be that the changes in the 'now' also makes changes in the future and maybe even changes the past or that it doesn't make changes and it just resolves to be in sync with what the future and the past requires of it. This model can work for the double slit mystery and for entangled particles, including where future actions may influence past events as predicted by physicist Asher Peres in 2000 and realized in a paper reporting the experiment published online April 22 in the journal Nature Physics, led by Xiao-song Ma of the Institute for Quantum Optics and Quantum Information at the University of Vienna.
Light is not a material object like a particle, it is radiation, or electro-magnetic energy.
Now, light can carry data or even mass, therefore it is mass.
Right?
But if it is matter, one could "hold it in his hand", right?
So, it is not matter, right?
But ... but ... it can hold data and mass???
That makes it matter, right??????
Well ... no.
Light ain't either, "yet both".
Light ... is LIGHT.
Well, also incorrect.
Light ain't light, at all.
The Lie That Is Light…
Or: How A Misinterpretation Became Doctrine.
Antwerp, June 5th, 1999
Introduction:
While we are being taught that light is light, science made a serious mistake, based on what we see on Earth.
While on Earth light is just that: light, it is therefore not in different places…
The Facts:
As we always have seen light as nothing more than that: light, we wrongly assumed that this is the case everywhere else…
Sure, wherever on Earth one is, there is light appearing as light.
Once we learned about space then, first through telescope, later through entering this cold, empty vastness, we saw a complete new form of Light (with a capital case as this is about the concept of Light, NOT light as in “a light”, same for the latter Dark) … “non-light Light” or simply… Dark!
If Light isn’t Light, then what is going on, what and how do we “see” this Light?
Light is a radio wave, like radiation, which in itself is “unseen” or Dark.
Once light gets to interact with matter, it excites this matter, making it basically shiny, if you like.
And this interaction of Dark with matter that created this shine, is what we visibly perceive as light.
Still, once light, even if interacting still with matter, enters a shadowy area, it turns Dark once more…
We are unconsciously aware that Light is not light, but we do neither think it over nor think it through, with causality in many areas of teachings, science, knowledge, wisdom and understanding.
Implications:
In a few areas, light is used as a tool:
1) Medical Profession = For discovery and diagnosis.
2) Chemistry.
3) Geology = Optical Mineralogy (using light to detect the optical properties of minerals).
4) Physics/Quantum Physics.
5) Engineering.
6) Astronomy.
, and even has a few fields based upon it, such as there be the Science of Light and Vision (Optics or Optometry), which is the study of Vision Impairment, which has 4 specifying classes:
1) Dispensing Optometry = the study of sight and the effect of lenses to help improvement in sight..
2) Refraction Optometry = Study of sight and testing sight .
3) Pathology Optometry = Study of the causes and causality of disease around, in and behind the eyes (nerves).
4) Medicinal Optometry = Optometry based on the use of diagnostic drugs and a limited range of therapy drugs.
The issue however is, that these use the concept of Light… as actual light.
In the most fundamentalistic ways, this is a wrong, an incorrect, an error.
Does this error has any impact on the fields where it is used or studied?
This, I cannot yet answer, but I will eventually as I dig deeper into the matter…
However: from a scholarly point of view, when one speaks of The Speed of Light, I begin to shiver, as it is so wrong in the deepest sense of it’s meaning and understanding: it is in it’s CORE ESSENCE literally SCIENTIFICALLY INCORRECT, and from a scientifically point of view unforgivable, hence I bring this matter to you.
Righting the Wrong:
Reasoning:
While it may not have much effect on the practical side (at least for now), this error makes a precedent:
As scientists we cannot be allowed to make mistakes, as mistakes can lead to devastating results.
Imagine: a Nuclear Medical Scientist needs to cut out a tumour in a patient’s brain, by the use of a new type of radiation-based laser that is extremely accurate with a stronger beam to do the job three times faster, which causes less side effects on the patient over longer time.
He sets the laser, pin-points it perfectly, but when he activated the laser, his arm sleeve slides a lever a tiny bit out of place, resulting in the beam missing the tumour by 1 millimetre.
Now, I hear you ask: “What is one millimetre?”
While burning away in someone’s skull, 1 millimetre can be the length between life or death… or worse: TOTAL paralysation while the patient keeps a perfectly sane and lively mind.
In case you do not quite get it: put Metallica – And Justice For all CD in your CD player and listen carefully to One…
What I am saying is: if we allow errors in naming concepts, then were will that lead to?
The concept of Science is to be ABSOLUTELY 100% accurate, right?
Even though it is in reality different, in mind it is about Absolutes, One either is, or is not.
From a point of interpreting the concept Science, mistakes are not allowed: it’s a form of Asperger Perfectionism.
And for us Asperger’s there’s only 0 or 1, no or yes, black or white: “Absolutes in Perfection = Perfect Absolutes”.
Ah, the simplicity of that what is.
A photon is no more than a way to present light in a less confusing way.
Light is not a material object like a particle, it is radiation, or electro-magnetic energy.
Light and quantum bits electrons etc are both particles and waves. A duality. EMR is photons and waves, both.
It has been, to my knowledge, suggested by serious science, No asserted, that a car (even) has a parallel wave function existing ...
A particle is a material state of something, like an electron, or a positron, ... , time, nor like, have material you can not hold it, or put it in a cup.Light and quantum bits electrons etc are both particles and waves. A duality. EMR is photons and waves, both.
It has been, to my knowledge, suggested by serious science, No asserted, that a car (even) has a parallel wave function existing ...
Thus, it is not a particle?
No?
well in principle yes you can put it in a cup. If you did so its wave function would collapse and it would be a particle. Previously though if no one decided otherwise it would be both a particle and a waveA particle is a material state of something, like an electron, or a positron, ... , time, nor like, have material you can not hold it, or put it in a cup.
Thus, it is not a particle?
No?
You can pour it in a cup, eh?
But theoretical.
So you cannot?
I can't see how light and time can be material of construction.
Energy, yes, Quantum energy, to be precise, but not a solid, a matter.
Light is known to be radiation, an electro-magnetic wave, which is non-material energy.
And for time, I believe it to be the same.
IF it was material, then all forces are material:
Gravity.
Weak Force.
Strong Force.
... .
That would be ... not good, I think?
But theoretical.
So you cannot?
I can't see how light and time can be material of construction.
Energy, yes, Quantum energy, to be precise, but not a solid, a matter.
Light is known to be radiation, an electro-magnetic wave, which is non-material energy.
And for time, I believe it to be the same.
IF it was material, then all forces are material:
Gravity.
Weak Force.
Strong Force.
... .
That would be ... not good, I think?
I can't see how light and time can be material of construction.
You can pour it in a cup, eh?
But theoretical.
So you cannot?
I can't see how light and time can be material of construction.
Energy, yes, Quantum energy, to be precise, but not a solid, a matter.
Light is known to be radiation, an electro-magnetic wave, which is non-material energy.
And for time, I believe it to be the same.
IF it was material, then all forces are material:
Gravity.
Weak Force.
Strong Force.
... .
No debate on this. Light is both a wave and a particle (photon)
A photon is NOT MATTER.No debate on this. Light is both a wave and a particle (photon)
No debate possible here.
It can carry energy and pass on energy, but it ain't material of construction, the photon, it is still immaterial.
Last edited:
A photon is NOT MATTER.
No debate possible here.
It can carry energy and pass on energy, but it ain't material of construction, the photon, it is still immaterial.
A photon is a particle. A wave is a wave. I do not understand your concentration on "immaterial". Light has mass. Electrons cannot be "pinned down" they also are both waves and particle. There are famous experiments e.g. the 2 slit experiment whereby light is directed toward two slits. It can act like waves (go through both slits and act like water waves) or be a particle and only go through one slit. Check out Quantum theory. In any event I don't see what the connection with time is.
Because many see a particle as a material object.
It is not.
So, I reacted to that, considering the above.
They have even shot buckyballs (C60 molecules) at a diffraction grating, and proved that they also make an interference pattern, just like laser does when you fire it at a grating.
Which further proves this.
Time then:
Many think, LIKE with light, one can pour it so to say in a cup, that you can hold it.
Even scientists.
Many terminology in Physics and QPhysics are moronic, and leads to severe misinterpretations.
For instance:
"Rest Mass".
"Imaginary Mass".
"Mass relative to whom it is that observes it". (REALLY?????? Relativity is one thing, this is total asylum on a completely new level).
This came from 4 different Physics ans 2 QPhysics teachers, mind.
So yeah, seen and heard a LOT that's out of reality.
By entire universes in lengths even.
In QPhysics there just ain't "material" particles.
See, I can't tell who you are, what you know, or how you interpret things.
So I reacted, not saying you misinterpreted anything, but not saying you had it right, either, simply since I do not know.
This was informational, not to "sort you out", or correct you.
But to all that reads this and begin to think time are like atoms or molecules (God-forbid).
Seems we're both on the same page, good.
It is not.
So, I reacted to that, considering the above.
They have even shot buckyballs (C60 molecules) at a diffraction grating, and proved that they also make an interference pattern, just like laser does when you fire it at a grating.
Which further proves this.
Time then:
Many think, LIKE with light, one can pour it so to say in a cup, that you can hold it.
Even scientists.
Many terminology in Physics and QPhysics are moronic, and leads to severe misinterpretations.
For instance:
"Rest Mass".
"Imaginary Mass".
"Mass relative to whom it is that observes it". (REALLY?????? Relativity is one thing, this is total asylum on a completely new level).
This came from 4 different Physics ans 2 QPhysics teachers, mind.
So yeah, seen and heard a LOT that's out of reality.
By entire universes in lengths even.
In QPhysics there just ain't "material" particles.
See, I can't tell who you are, what you know, or how you interpret things.
So I reacted, not saying you misinterpreted anything, but not saying you had it right, either, simply since I do not know.
This was informational, not to "sort you out", or correct you.
But to all that reads this and begin to think time are like atoms or molecules (God-forbid).
Seems we're both on the same page, good.
Last edited:
Just because there is no mass, does not mean that it's not material. As a matter of fact, in the future, the strongest and the densest material ever made, might come from the superposition of fields. In theory, fields can become much stronger and denser than any mass.
A particle is a particle. It has configured, confined, motion. The motion is confined by an EM field. We can not superposition mass. But, we can cut the EM field from the particle.
And add many more cut fields to it. To where the fields, are much more dense then any mass.
There are two materials. Mass material, and field material. An electric field or a magnetic field is just as real and material........as any mass. The superposition of the particle EM fields, is what bonds particles together.
When you look up at the stars, you are looking at superposition........not mass. The mass that emitted those lights, are no longer there. But the field superposition is still there.
A particle is a particle. It has configured, confined, motion. The motion is confined by an EM field. We can not superposition mass. But, we can cut the EM field from the particle.
And add many more cut fields to it. To where the fields, are much more dense then any mass.
There are two materials. Mass material, and field material. An electric field or a magnetic field is just as real and material........as any mass. The superposition of the particle EM fields, is what bonds particles together.
When you look up at the stars, you are looking at superposition........not mass. The mass that emitted those lights, are no longer there. But the field superposition is still there.
"Just because there is no mass, does not mean that it's not material. As a matter of fact, in the future, the strongest and the densest material ever made, might come from the superposition of fields. In theory, fields can become much stronger and denser than any mass. "
Yep, Roddenberry was a genius: Replicators.
Matter "out of nowhere" (energy).
Once however it enters a material state it becomes Relativistic of nature, Quantum in BENEATH the level of all that is matter.
It is the base form, or if you like, the Force in Star Wars, bit silly an analogy, but not untrue.
Quantum is not relativistic of level, and should not be implemented in Relativity!
It PRECEDED Relativity, it came forth out of Quantum.
Before Relativistic effects, there was Quantum in that Singularity.
ALL in base form is Quantum Energy, be it other energies resulting from matter or matter itself: the matter is nothing more than energy formed into.
It is being added to Relativity, or, they try to, but they will not be able to.
It is the base of Relativity, all relative is consequence of Quantum Energy, thus it exists below the level of Relativity.
One should stop trying to “relativise” Quantum Energy, see this on it’s own.
It’s like a car that crashes:
Let’s see this as relativity.
The car being made is not part of the crash, yet related to this.
Since, if the car was not made, it could not ride, thus not crash.
The creation of the car is the Quantum Energy:
The “starter level” of the crash.
An odd analogy, yes.
But I think, it’s not that incorrect.
Though, I should have gone deeper even, where the metal and oil (plastic) was still in base form.
But that explanation of processes would have taken too long I think (digging up, purification, …).
But you get the point.
"There are two materials. Mass material, and field material. An electric field or a magnetic field is just as real and material........as any mass. The superposition of the particle EM fields, is what bonds particles together. "
What are we speaking of: QP or P/RT?
You seem to bring both levels together as if they belong together?
"A particle is a particle. It has configured, confined, motion. The motion is confined by an EM field. We can not superposition mass. But, we can cut the EM field from the particle. "
Mass it not therefore matter.
"When you look up at the stars, you are looking at superposition........not mass. The mass that emitted those lights, are no longer there. But the field superposition is still there. "
Excuse me?
Stars are MASS, MATERIAL.
Our sun is a soup of atoms, Superplasma in material state.
It brings forth energy, yes.
But these are not just compressed energy.
For the record:
Plasma is a matter state, the current states known are, but not limited to:
There are actually a “few” more states:
01) Solids: A solid holds a definite shape and volume without a container. The particles are held very close to each other.
02) Amorphous Solid: A solid in which there is no far-range order of the positions of the atoms.
03) Crystalline Solid: A solid in which atoms, molecules, or ions are packed in regular order.
04) Plastic Crystal: A Molecular Solid with long-range positional order but with constituent molecules retaining rotational freedom.
05) Quasi-Crystal: A solid in which the positions of the atoms have long-range order, but this is not in a repeating pattern.
06) Liquid: A mostly Non-Compressible Fluid. Able to conform to the shape of its container but retains a (nearly) constant volume independent of pressure.
07) Liquid Crystal: Properties intermediate between Liquids and Crystals. Generally, able to flow like a Liquid but exhibiting long-range order.
08) Non-Newtonian Fluid: a fluid that does not follow Newton's law of viscosity.
09) Gas: A compressible fluid. Not only will a gas conform to the shape of its container but it will also expand to fill the container.
10) Plasma: Free charged Particles, usually in equal numbers, such as Ions and Electrons. Unlike Gases, Plasma may self-generate magnetic fields and electric currents, and respond strongly and collectively to electromagnetic forces. Plasma is very uncommon on Earth (except for the ionosphere), although it is the most common state of matter in the universe.[1]
11) Supercritical Fluid: At sufficiently high temperatures and pressures, the distinction between Liquid and Gas disappears.
12) Degenerate Matter: matter under very high pressure, supported by the “Pauli Exclusion Principle”.
13) Electron-Degenerate Matter: found inside White Dwarf Stars. Electrons remain bound to atoms but are able to transfer to adjacent atoms.
14) Neutron-Degenerate Matter: found in Neutron Stars. Vast gravitational pressure compresses atoms so strongly that the electrons are forced to combine with protons via Inverse β-decay, resulting in a super dense conglomeration of Neutrons. (Normally free Neutrons outside an Atomic Nucleus will decay with a half-life of just under 15 minutes, but in a Neutron Star, as in the Nucleus of an atom, other effects stabilize the Neutrons.)
15) Strange Matter: (The HELL kind of a moronic name is that? Which idiot figured, this is a “cool name”?) A type of Quark Matter that may exist inside some Neutron Stars close to the Tolman–Oppenheimer–Volkoff Limit (approximately 2–3 solar masses). May be stable at lower energy states once formed.
16) Quantum Spin Hall State: a theoretical phase that may pave the way for the development of electronic devices that dissipate less energy and generate less heat. This is a derivation of the Quantum Hall State of matter.
17) Bose–Einstein Condensate: a phase in which a large number of Bosons all inhabit the same Quantum State, in effect becoming one Single Wave/Particle. This is a low-energy phase that can only be formed in laboratory conditions and very cold temperatures (This means, on Earth, this state might be found in other places under the right natural conditions). It must be close to zero Kelvin, or Absolute Zero. Satyendra Nath Bose, and Einstein predicted the existence of such a state in the 1920s, but it was not observed until 1995 by Eric Cornell and Carl Wieman.
18) Fermionic Condensate: Similar to the Bose-Einstein Condensate but composed of Fermions, also known as Fermi-Dirac Condensate. The Pauli Exclusion Principle prevents Fermions from entering the same Quantum State, but a pair of Fermions can behave like a Boson, and multiple such pairs can then enter the same Quantum State without restriction.
SUPPLEMENTAL YET IMPORTANT!
18b) Electron quadruplets: a proven phenomenon (2021, observations consistent with electron quadrupling using "Hole-Doped Ba1-xKxFe2As.). In a Matter Exotic State, Cooper Pairs do not exhibit Long-Range Order. Electron, then, Quadruplets do. Named "Quartic Metal Phase" is related to, BUT DISTINCT TO, those Superconductors explained in Standard BCS Theory, "rather than expelling magnetic field lines as in the Meissner effect, it generates them, a spontaneous Nernst effect that indicates the breaking of time-reversal symmetry."
19) Superconductivity: A phenomenon of exactly zero electrical resistance and expulsion of magnetic fields occurring in certain materials when cooled below a characteristic critical temperature. Superconductivity is the ground state of many elemental metals.
20) Superfluid: A phase achieved by a few Cryogenic Liquids at extreme temperature at which they become able to flow without friction. A Superfluid can flow up the side of an open container and down the outside. Placing a Superfluid in a spinning container will result in Quantized Vortices.
21) Superplasma: NOT YET FOUND/MADE, I am, however, darn sure it is “out there”.
22) Supersolid: similar to a superfluid, a Supersolid can move without friction but retains a rigid shape.
23) Quantum Spin Liquid: A disordered state in a system of Interacting Quantum Spins which preserves its disorder to very low temperatures, unlike other disordered states.
24) Heavy Fermion Materials: Heavy Fermion Materials or Strongly Correlated Fermi Systems form a new state of matter that defines by Quantum Phase Transitions, and exhibits a universal scaling behaviour of its Thermo-Dynamica, transport and relaxation properties. Quantum Spin Liquid, Quasi-Crystals, 2D Fermi Liquids, Heavy-Fermion Metals and Heavy-Fermion Superconductors can belong to the new state of matter.
25) String-Net Liquid: Atoms in this state have apparently unstable arrangements, like a Liquid, but are still consistent in the overall pattern, like a Solid.
26) Dropleton: An artificial Quasi-Particle, constituting a collection of Electrons and holes inside a Semi-Conductor. The Dropleton is the first known Quasi-Particle that behaves like a Liquid.
27) Time Crystals: A state of matter where an object can have movement even at its lowest energy state.
28) Rydberg Polaron: A state of matter that can only exist at ultra-low temperatures and consists of atoms inside of atoms.
HIGH ENERGY STATES:
01) Quark–Gluon Plasma: A phase in which Quarks become free and able to move independently (rather than being perpetually bound into Particles, or bound to each other in a Quantum-Lock where exerting force adds energy and eventually solidifies into new Quark) in an ocean of Gluons (Sub-Atomic Particles that transmit the strong force that binds Quarks together). May be briefly attainable in Particle Accelerators, or possibly inside Neutron Stars.
--------------------------------------------------------------------------------------------------------------------------------------
Oh well, let us add:
☣☣☣ Other states: ☣☣☣
Colloid
Glass
Crystal
Liquid Crystal
Time Crystal
Quantum Spin Liquid
Exotic Matter (Ugh, another such brilliant name)
Programmable Matter
Dark Matter
Antimatter
☣Magnetically Ordered☣
Anti-Ferromagnet
Ferrimagnet
Ferromagnet
String-net Liquid
Superglass
☣☣☣ Phase-Transition ☣☣☣
Boiling
Boiling Point
Condensation
Critical Line
Critical Point
Crystallization
Deposition
Evaporation
Flash Evaporation
Freezing
Chemical Ionization
Ionization
Lambda Point
Melting
Melting Point
Recombination
Regelation
Saturated Fluid
Sublimation
Supercooling
Triple Point
Vaporization
Vitrification
☣☣☣ Quantities ☣☣☣
Enthalpy of Fusion
Enthalpy of Sublimation
Enthalpy of Vaporization
Latent Heat
Latent Internal Energy
Trouton's Rule
Volatility
☣☣☣ Concepts ☣☣☣
Baryonic Matter
Binodal
Compressed Fluid
Cooling Curve
Equation of State
Leidenfrost Effect
Macroscopic Quantum Phenomena
Mpemba Effect
Order and Disorder (Physics/Chaos Theory)
Spinodal
Superconductivity|
Superheated Vapour
Superheating
Thermo-Dielectric Effect
Sorry to not be too in-depth for the latter added states.
Please Google explanations where needed, I am not too eager nor have the time to write the entire day here to this post.
Other sites do require a tad of attention, too.
Thank you.
Few edits to get rid of a few typos.
Sorry.
Been typing fast, leading to error.
Hurry ain't ever good.
Found another one:
Concepts is not a state.
Yep, Roddenberry was a genius: Replicators.
Matter "out of nowhere" (energy).
Once however it enters a material state it becomes Relativistic of nature, Quantum in BENEATH the level of all that is matter.
It is the base form, or if you like, the Force in Star Wars, bit silly an analogy, but not untrue.
Quantum is not relativistic of level, and should not be implemented in Relativity!
It PRECEDED Relativity, it came forth out of Quantum.
Before Relativistic effects, there was Quantum in that Singularity.
ALL in base form is Quantum Energy, be it other energies resulting from matter or matter itself: the matter is nothing more than energy formed into.
It is being added to Relativity, or, they try to, but they will not be able to.
It is the base of Relativity, all relative is consequence of Quantum Energy, thus it exists below the level of Relativity.
One should stop trying to “relativise” Quantum Energy, see this on it’s own.
It’s like a car that crashes:
Let’s see this as relativity.
The car being made is not part of the crash, yet related to this.
Since, if the car was not made, it could not ride, thus not crash.
The creation of the car is the Quantum Energy:
The “starter level” of the crash.
An odd analogy, yes.
But I think, it’s not that incorrect.
Though, I should have gone deeper even, where the metal and oil (plastic) was still in base form.
But that explanation of processes would have taken too long I think (digging up, purification, …).
But you get the point.
"There are two materials. Mass material, and field material. An electric field or a magnetic field is just as real and material........as any mass. The superposition of the particle EM fields, is what bonds particles together. "
What are we speaking of: QP or P/RT?
You seem to bring both levels together as if they belong together?
"A particle is a particle. It has configured, confined, motion. The motion is confined by an EM field. We can not superposition mass. But, we can cut the EM field from the particle. "
Mass it not therefore matter.
"When you look up at the stars, you are looking at superposition........not mass. The mass that emitted those lights, are no longer there. But the field superposition is still there. "
Excuse me?
Stars are MASS, MATERIAL.
Our sun is a soup of atoms, Superplasma in material state.
It brings forth energy, yes.
But these are not just compressed energy.
For the record:
Plasma is a matter state, the current states known are, but not limited to:
There are actually a “few” more states:
01) Solids: A solid holds a definite shape and volume without a container. The particles are held very close to each other.
02) Amorphous Solid: A solid in which there is no far-range order of the positions of the atoms.
03) Crystalline Solid: A solid in which atoms, molecules, or ions are packed in regular order.
04) Plastic Crystal: A Molecular Solid with long-range positional order but with constituent molecules retaining rotational freedom.
05) Quasi-Crystal: A solid in which the positions of the atoms have long-range order, but this is not in a repeating pattern.
06) Liquid: A mostly Non-Compressible Fluid. Able to conform to the shape of its container but retains a (nearly) constant volume independent of pressure.
07) Liquid Crystal: Properties intermediate between Liquids and Crystals. Generally, able to flow like a Liquid but exhibiting long-range order.
08) Non-Newtonian Fluid: a fluid that does not follow Newton's law of viscosity.
09) Gas: A compressible fluid. Not only will a gas conform to the shape of its container but it will also expand to fill the container.
10) Plasma: Free charged Particles, usually in equal numbers, such as Ions and Electrons. Unlike Gases, Plasma may self-generate magnetic fields and electric currents, and respond strongly and collectively to electromagnetic forces. Plasma is very uncommon on Earth (except for the ionosphere), although it is the most common state of matter in the universe.[1]
11) Supercritical Fluid: At sufficiently high temperatures and pressures, the distinction between Liquid and Gas disappears.
12) Degenerate Matter: matter under very high pressure, supported by the “Pauli Exclusion Principle”.
13) Electron-Degenerate Matter: found inside White Dwarf Stars. Electrons remain bound to atoms but are able to transfer to adjacent atoms.
14) Neutron-Degenerate Matter: found in Neutron Stars. Vast gravitational pressure compresses atoms so strongly that the electrons are forced to combine with protons via Inverse β-decay, resulting in a super dense conglomeration of Neutrons. (Normally free Neutrons outside an Atomic Nucleus will decay with a half-life of just under 15 minutes, but in a Neutron Star, as in the Nucleus of an atom, other effects stabilize the Neutrons.)
15) Strange Matter: (The HELL kind of a moronic name is that? Which idiot figured, this is a “cool name”?) A type of Quark Matter that may exist inside some Neutron Stars close to the Tolman–Oppenheimer–Volkoff Limit (approximately 2–3 solar masses). May be stable at lower energy states once formed.
16) Quantum Spin Hall State: a theoretical phase that may pave the way for the development of electronic devices that dissipate less energy and generate less heat. This is a derivation of the Quantum Hall State of matter.
17) Bose–Einstein Condensate: a phase in which a large number of Bosons all inhabit the same Quantum State, in effect becoming one Single Wave/Particle. This is a low-energy phase that can only be formed in laboratory conditions and very cold temperatures (This means, on Earth, this state might be found in other places under the right natural conditions). It must be close to zero Kelvin, or Absolute Zero. Satyendra Nath Bose, and Einstein predicted the existence of such a state in the 1920s, but it was not observed until 1995 by Eric Cornell and Carl Wieman.
18) Fermionic Condensate: Similar to the Bose-Einstein Condensate but composed of Fermions, also known as Fermi-Dirac Condensate. The Pauli Exclusion Principle prevents Fermions from entering the same Quantum State, but a pair of Fermions can behave like a Boson, and multiple such pairs can then enter the same Quantum State without restriction.
SUPPLEMENTAL YET IMPORTANT!
18b) Electron quadruplets: a proven phenomenon (2021, observations consistent with electron quadrupling using "Hole-Doped Ba1-xKxFe2As.). In a Matter Exotic State, Cooper Pairs do not exhibit Long-Range Order. Electron, then, Quadruplets do. Named "Quartic Metal Phase" is related to, BUT DISTINCT TO, those Superconductors explained in Standard BCS Theory, "rather than expelling magnetic field lines as in the Meissner effect, it generates them, a spontaneous Nernst effect that indicates the breaking of time-reversal symmetry."
19) Superconductivity: A phenomenon of exactly zero electrical resistance and expulsion of magnetic fields occurring in certain materials when cooled below a characteristic critical temperature. Superconductivity is the ground state of many elemental metals.
20) Superfluid: A phase achieved by a few Cryogenic Liquids at extreme temperature at which they become able to flow without friction. A Superfluid can flow up the side of an open container and down the outside. Placing a Superfluid in a spinning container will result in Quantized Vortices.
21) Superplasma: NOT YET FOUND/MADE, I am, however, darn sure it is “out there”.
22) Supersolid: similar to a superfluid, a Supersolid can move without friction but retains a rigid shape.
23) Quantum Spin Liquid: A disordered state in a system of Interacting Quantum Spins which preserves its disorder to very low temperatures, unlike other disordered states.
24) Heavy Fermion Materials: Heavy Fermion Materials or Strongly Correlated Fermi Systems form a new state of matter that defines by Quantum Phase Transitions, and exhibits a universal scaling behaviour of its Thermo-Dynamica, transport and relaxation properties. Quantum Spin Liquid, Quasi-Crystals, 2D Fermi Liquids, Heavy-Fermion Metals and Heavy-Fermion Superconductors can belong to the new state of matter.
25) String-Net Liquid: Atoms in this state have apparently unstable arrangements, like a Liquid, but are still consistent in the overall pattern, like a Solid.
26) Dropleton: An artificial Quasi-Particle, constituting a collection of Electrons and holes inside a Semi-Conductor. The Dropleton is the first known Quasi-Particle that behaves like a Liquid.
27) Time Crystals: A state of matter where an object can have movement even at its lowest energy state.
28) Rydberg Polaron: A state of matter that can only exist at ultra-low temperatures and consists of atoms inside of atoms.
HIGH ENERGY STATES:
01) Quark–Gluon Plasma: A phase in which Quarks become free and able to move independently (rather than being perpetually bound into Particles, or bound to each other in a Quantum-Lock where exerting force adds energy and eventually solidifies into new Quark) in an ocean of Gluons (Sub-Atomic Particles that transmit the strong force that binds Quarks together). May be briefly attainable in Particle Accelerators, or possibly inside Neutron Stars.
--------------------------------------------------------------------------------------------------------------------------------------
Oh well, let us add:
☣☣☣ Other states: ☣☣☣
Colloid
Glass
Crystal
Liquid Crystal
Time Crystal
Quantum Spin Liquid
Exotic Matter (Ugh, another such brilliant name)
Programmable Matter
Dark Matter
Antimatter
☣Magnetically Ordered☣
Anti-Ferromagnet
Ferrimagnet
Ferromagnet
String-net Liquid
Superglass
☣☣☣ Phase-Transition ☣☣☣
Boiling
Boiling Point
Condensation
Critical Line
Critical Point
Crystallization
Deposition
Evaporation
Flash Evaporation
Freezing
Chemical Ionization
Ionization
Lambda Point
Melting
Melting Point
Recombination
Regelation
Saturated Fluid
Sublimation
Supercooling
Triple Point
Vaporization
Vitrification
☣☣☣ Quantities ☣☣☣
Enthalpy of Fusion
Enthalpy of Sublimation
Enthalpy of Vaporization
Latent Heat
Latent Internal Energy
Trouton's Rule
Volatility
☣☣☣ Concepts ☣☣☣
Baryonic Matter
Binodal
Compressed Fluid
Cooling Curve
Equation of State
Leidenfrost Effect
Macroscopic Quantum Phenomena
Mpemba Effect
Order and Disorder (Physics/Chaos Theory)
Spinodal
Superconductivity|
Superheated Vapour
Superheating
Thermo-Dielectric Effect
Sorry to not be too in-depth for the latter added states.
Please Google explanations where needed, I am not too eager nor have the time to write the entire day here to this post.
Other sites do require a tad of attention, too.
Thank you.
Few edits to get rid of a few typos.
Sorry.
Been typing fast, leading to error.
Hurry ain't ever good.
Found another one:
Concepts is not a state.
Last edited:
Similar threads
- Replies
- 3
- Views
- 233
- Replies
- 0
- Views
- 355
- Replies
- 10
- Views
- 2K
- Replies
- 6
- Views
- 3K
- Replies
- 7
- Views
- 2K
TRENDING THREADS
-
Why does striking flint against steel start a fire?
- Started by admin
- Replies: 3
-
George Washington's stash of centuries-old cherries found hidden under Mount Vernon floor
- Started by admin
- Replies: 14
-
What is a living individual and is it naturally universally mobile?
- Started by tonylang
- Replies: 138
-

Live Science is part of Future plc, an international media group and leading digital publisher. Visit our corporate site.
© Future Publishing Limited Quay House, The Ambury, Bath BA1 1UA. All rights reserved. England and Wales company registration number 2008885.
