Ahmed Farag and Saurya Das offer two papers explaining a non-singularity based theory of the universe which shows the universe having an infinite age.
Between the information contained in these two papers, I've included an explanation of the leading paper from physics.org.
When we discuss the Big Bang vs. the infinite steady state theories, I think that these papers, of the many to be found on this topic, offer the most easily understood with the most robust mathematical and physical framework.
This is not to say that I completely agree with the steady state of an infinite age theory, because I've been in agreement with Einstein's theories.
Higher mathematics combined with a greater ability to provide data to be crunched from ever more complicated and far more effective gathering of the electromagnetic spectrum from improved orbital, ground stationary and now, with the JWST located at Lagrange Point 2, may yet yield the incontrovertible evidence needed to either overthrow Einstein and his theories or further enshrine them. And, they may also yield results falling somewhere in the middle ground.
Cosmology from quantum potential
by Ahmed Farag Ali 1,2 ∗ and Saurya Das 3 †
1. Center for Theoretical Physics,
Zewail City of Science and Technology, Giza, 12588, Egypt.
2. Dept. of Physics, Faculty of Sciences, Benha University, Benha, 13518, Egypt. and
3. Department of Physics and Astronomy, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta, Canada T1K 3M4
It was shown recently that replacing classical geodesics with quantal (Bohmian) trajectories gives rise to a quantum corrected Raychaudhuri equation (QRE). In this article we derive the second order Friedmann equations from the QRE, and show that this also contains a couple of quantum correction terms, the first of which can be interpreted as cosmological constant (and gives a correct estimate of its observed value), while the second as a radiation term in the early universe, which gets rid of the big-bang singularity and predicts an infinite age of our universe.
The generally accepted view of our universe (homogeneous, isotropic, spatially flat, obeying general relativity, and currently consisting of about 72% Dark Energy, likely in the form of a cosmological constant Λ, about 23% Dark Matter, and the rest observable matter), implies its small acceleration, as inferred from Type IA supernova observations, CMBR data and baryon acoustic oscillations. However, quite a few things remain to be better understood, e.g.:
(i) the smallness of Λ, about 10−123 in Planck units (‘the smallness problem’),
(ii) the approximate equality of vacuum and matter density in the current epoch (‘the coincidence problem’),
(iii) the apparent extreme fine-tuning required in the early universe, to have a spatially flat universe in the current epoch (‘the flatness problem’),
(iv) the true nature of dark matter, and
(v) the beginning of our universe, or the so-called big- bang.
In summary, we have shown here that as for the QRE, the second order Friedmann equation derived from the QRE also contains two quantum correction terms. These terms are generic and unavoidable and follow naturally in a quantum mechanical description of our universe. Of these, the first can be interpreted as cosmological con- stant or dark energy of the correct (observed) magnitude and a small mass of the graviton (or axion). The second quantum correction term pushes back the time singu- larity indefinitely, and predicts an everlasting universe. While inhomogeneous or anisotropic perturbations are not expected to significantly affect these results, it would be useful to redo the current study with such small per- turbations to rigorously confirm that this is indeed the case. Also, as noted in the introduction, we assume it to follow general relativity, whereas the Einstein equations may themselves undergo quantum corrections, especially at early epochs, further affecting predictions. Given the robust set of starting assumptions, we expect our main results to continue to hold even if and when a fully satis- factory theory of quantum gravity is formulated. For the cosmological constant problem at late times on the other hand, quantum gravity effects are practically absent and can be safely ignored. We hope to report on these and related issues elsewhere.
See: https://arxiv.org/pdf/1404.3093v3.pdf
No Big Bang? Quantum equation predicts universe has no beginning
by Lisa Zyga , Phys.org
February 9, 2015
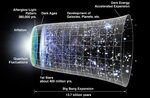
This is an artist's concept of the metric expansion of space, where space (including hypothetical non-observable portions of the universe) is represented at each time by the circular sections. Note on the left the dramatic expansion (not to scale) occurring in the inflationary epoch, and at the center the expansion acceleration. The scheme is decorated with WMAP images on the left and with the representation of stars at the appropriate level of development. Credit: NASA
The universe may have existed forever, according to a new model that applies quantum correction terms to complement Einstein's theory of general relativity. The model may also account for dark matter and dark energy, resolving multiple problems at once.
The widely accepted age of the universe, as estimated by general relativity, is 13.8 billion years. In the beginning, everything in existence is thought to have occupied a single infinitely dense point, or singularity. Only after this point began to expand in a "Big Bang" did the universe officially begin.
Although the Big Bang singularity arises directly and unavoidably from the mathematics of general relativity, some scientists see it as problematic because the math can explain only what happened immediately after—not at or before—the theorized singularity.
"The Big Bang singularity is the most serious problem of general relativity because the laws of physics appear to break down there," Ahmed Farag Ali at Benha University and the Zewail City of Science and Technology, both in Egypt, told Phys.org.
Ali and coauthor Saurya Das at the University of Lethbridge in Alberta, Canada, have shown in a paper published in Physics Letters B that the Big Bang singularity can be resolved by their new model in which the universe has no beginning and no end.
Old ideas revisited
The physicists emphasize that their quantum correction terms are not applied ad hoc in an attempt to specifically eliminate the Big Bang singularity. Their work is based on ideas by the theoretical physicist David Bohm, who is also known for his contributions to the philosophy of physics. Starting in the 1950s, Bohm explored replacing classical geodesics (the shortest path between two points on a curved surface) with quantum trajectories.
In their paper, Ali and Das applied these Bohmian trajectories to an equation developed in the 1950s by physicist Amal Kumar Raychaudhuri at Presidency University in Kolkata, India. Raychaudhuri was also Das's teacher when he was an undergraduate student of that institution in the '90s.
Using the quantum-corrected Raychaudhuri equation, Ali and Das derived quantum-corrected Friedmann equations, which describe the expansion and evolution of universe (including the Big Bang) within the context of general relativity. Although it's not a true theory of quantum gravity, the model does contain elements from both quantum theory and general relativity. Ali and Das also expect their results to hold even if and when a full theory of quantum gravity is formulated.
No singularities nor dark stuff
In addition to not predicting a Big Bang singularity, the new model does not predict a "big crunch" singularity, either. In general relativity, one possible fate of the universe is that it starts to shrink until it collapses in on itself in a big crunch and becomes an infinitely dense point once again.
Ali and Das explain in their paper that their model avoids singularities because of a key difference between classical geodesics and Bohmian trajectories. Classical geodesics eventually cross each other, and the points at which they converge are singularities. In contrast, Bohmian trajectories never cross each other, so singularities do not appear in the equations.
In cosmological terms, the scientists explain that the quantum corrections can be thought of as a cosmological constant term (without the need for dark energy) and a radiation term. These terms keep the universe at a finite size, and therefore give it an infinite age. The terms also make predictions that agree closely with current observations of the cosmological constant and density of the universe.
New gravity particle
In physical terms, the model describes the universe as being filled with a quantum fluid. The scientists propose that this fluid might be composed of gravitons—hypothetical massless particles that mediate the force of gravity. If they exist, gravitons are thought to play a key role in a theory of quantum gravity.
In a related paper, Das and another collaborator, Rajat Bhaduri of McMaster University, Canada, have lent further credence to this model. They show that gravitons can form a Bose-Einstein condensate (named after Einstein and another Indian physicist, Satyendranath Bose) at temperatures that were present in the universe at all epochs.
Motivated by the model's potential to resolve the Big Bang singularity and account for dark matter and dark energy, the physicists plan to analyze their model more rigorously in the future. Their future work includes redoing their study while taking into account small inhomogeneous and anisotropic perturbations, but they do not expect small perturbations to significantly affect the results.
"It is satisfying to note that such straightforward corrections can potentially resolve so many issues at once," Das said.
See: https://phys.org/news/2015-02-big-quantum-equation-universe.html
Dark matter and dark energy from Bose-Einstein condensate
March 25, 2015
by Saurya Das 1∗ and Rajat K. Bhaduri2†
1. Department of Physics and Astronomy, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta, Canada T1K 3M4
2. Department of Physics and Astronomy, McMaster University, Hamilton, Ontario, Canada L8S 4M1
We show that Dark Matter consisting of bosons of mass of about 1 eV or less has critical tem- perature exceeding the temperature of the universe at all times, and hence would have formed a Bose-Einstein condensate at very early epochs. We also show that the wavefunction of this condensate, via the quantum potential it produces, gives rise to a cosmological constant which may account for the correct dark energy content of our universe. We argue that massive gravitons or axions are viable candidates for these constituents. In the far future this condensate is all that remains of our universe.
In this paper we show that if dark matter (DM) is assumed to consist of a gas of bosons of mass m, then for m ≤ 1eV , the critical temperature below which they will form a Bose-Einstein condensate (BEC) exceeds the temperature of the universe at all times. Therefore they would form such a condensate at very early epochs, in which a macroscopic fraction of the bosons fall to the ground state with little or no momentum and zero pressure, and therefore may be considered as viable candidates for cold dark matter (CDM). Further, via the quantum po- tential that it produces, the macroscopic wavefunction of the condensate gives rise to a positive cosmological constant in the Friedmann equation, whose magnitude depends on m, and for m ≃ 10−32 eV , one obtains the observed value of the cosmological constant. Therefore bosons with this tiny mass can account for both DM and dark energy (DE) in our universe. We argue that massive gravitons or axions are viable candidates for these bosons. Finally we speculate on the ultimate fate of our universe, and end with some open problems.
In summary, we have shown here that bosons of tiny mass should form a Bose-Einstein condensate (BEC) at early times and may account for the DM content of the universe, while its macro- scopic wavefunction can account for the DE. Both mas- sive gravitons and axions are viable candidates of bosons of this mass, and hence that of DM and DE. While the former requires a modification of general relativity, the latter requires extension of the standard model.
While this picture predicts a high degree of homogeneity and isotropy at large scales (as observed), it still allows for relatively small variations of densities, temperatures etc. at smaller scales. It will be interesting to investigate other testable predictions of this BEC, such as its heat capacity, the distribution of DM, response to galaxy ro- tations etc. We hope to report on these elsewhere.
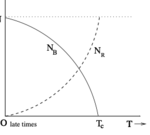
FIG. 1: NB and NR vs. T. .
Note added
In this note we list features of previous works in BEC in the context of cosmology. In [9], the authors use the same formula for Tc as our Eq.(1), and conjectured that the infinite heat conductivity of the BEC may account for the uniform microwave background temperature. In [10], it was proposed that the BEC manifests itself as DE and DM at different epochs. In [11], DM candidate of a BEC formed out of the ‘phion’ field in modified gravity was considered. In [12], a cold star composed of a dilute BEC was studied. In [13], [16], [17], [18], [20] and [21], properties of various forms of BEC DM were studied. In [14] and [24], the possibility of axions as a BEC was examined. Background geometries and black holes made up of BEC were considered in [15]. DM composed of a BEC of particles obeying infinite statistics was studied in [19]. In [22] BEC in loop quantum cosmology was studied. In [23] it was shown that DM can be well approximated by BEC at large scales, although their estimate of boson mass was higher than that proposed in this paper.
See: https://arxiv.org/pdf/1411.0753.pdf
Bose-Einstein condensate in cosmology
August 30, 2018
Saurya Das (U. Lethbridge), R. K. Bhaduri (McMaster U.)
matter (DM) and dark energy (DE). Whereas DM holds
the rotating galaxies together, DE makes the expanding
universe accelerate. In accounting for the distribution
of mass/energy in the universe, visible hadronic matter
and radiation contribute only about five percent, DM
about twenty five percent, while the rest, a whopping
seventy percent, comes from DE . To start with, the constituents of DE are not known, despite viable candidates such as the cosmological constant and a dynamical scalar field. The constituents of DM are not known either. There has been many studies invoking weakly in- teracting massive particles (WIMPs) that may form cold DM. Not only does it have shortcomings in reproducing the DM density profiles within a galaxy, no such particle has been experimentally found. Other DM candidates include solitons, massive compact (halo) objects, primordial black holes, gravitons etc. They have similar shortcomings.
Given that DM is all-pervading, cold and dark, and clumped near galaxies, we pose the following question: can it be a giant BEC, of cosmological length scales? Following the paper by Bose which laid the foundations of Bose-Einstein statistics [9], Einstein predicted that a gas of bosons will form a BEC at sufficiently low tem- peratures [10]. Here we show that following an earlier proposal by the current authors:
(i) a sea of weakly interacting light bosons can form a BEC, preserving large scale homogeneity and isotropy, and be a viable DM candidate, as long as the mass of each constituent does not exceed a few eV/c2 2, and
(ii) the quantum potential associated with the above BEC can also explain DE.
Note that in a BEC, the bosons are in the lowest energy state that is nearly at zero energy, even if outside the condensate the bosons are highly relativistic due to its low mass. We should point out that BEC model for DM has been studied by many authors in the past. For example, one can consider a scalar field dark matter (SFDM) that invokes spin zero ultralight bosons whose Compton wave length spans cosmic distances. But as mentioned earlier, the novel aspect of our model is that it also provides us with a viable source of DE. In this semi-technical article, we present the bulk of our work in an elementary fashion using Newtonian dynamics, after staging the backdrop of the cosmological model.
There has been many studies invoking weakly in- teracting massive particles (WIMPs) that may form cold DM. Not only does it have shortcomings in reproducing the DM density profiles within a galaxy, no such par- ticle has been experimentally found. Other DM candidates include solitons, massive compact (halo) objects, primordial black holes, gravitons etc. They have similar shortcomings.
Given that DM is all-pervading, cold and dark, and clumped near galaxies, we pose the following question: can it be a giant BEC, of cosmological length scales? Following the paper by Bose which laid the foundations of Bose-Einstein statistics, Einstein predicted that a gas of bosons will form a BEC at sufficiently low temperatures.
See: https://arxiv.org/pdf/1808.10505.pdf
See: https://link.springer.com/article/10.1140/epjc/s10052-016-4182-x
When you consider a universe following the standard Einstein cosmology, the dynamics of the universe is described by Einstein's general relativity equations, one can see that there exists a mysterious singularity at the beginning of time, the so-called big bang. This singularity may be considered as a deficiency of Einstein cosmology at high energies. Actually, you may assert that the big bang implies the breakdown of general relativity at scales with high energies, whereas we know from the observational evidence, such as the existence of the cosmic microwave background, that the big bang model works at scales lower than Planck energy scale. At these scales, the universe was full of a hot photon–baryon combination almost described as a radiation fluid. This hot combination was cooling down as the universe was experiencing the expansion, and due to the different scaling behaviors of pure radiation and pure matter, the energy density of non-relativistic matter started to dominate over the energy density of radiation and led to the formation of structures, which we see today as the galactic filaments and the cosmic web.
In the Bose–Einstein Condensation (BEC) model, the dark matter can be described as a non-relativistic Newtonian gravitational condensate, whose pressure and energy density are related by a barotropic equation of state. Based on the above arguments, we assume the possibility that the Bose–Einstein condensation might have happened during the early stages of cosmological evolution of the universe with a temperature comparable to the critical temperature for Bose–Einstein condensation, where m is the particle mass, n is the particle density, and 𝑘BkB is Boltzmann’s constant.
If you assume there are two phases of dark matter, one as the bosonic particles before BEC, and the other one as BEC dark matter, you might ask: “is there any experimental indication for the occurrence of BEC, the existence of these two phases, and the preference of one to the other one?” and “why is it necessary to distinguish ordinary dark matter from BEC dark matter?” Of course, at present there is no direct evidence for the occurrence of BEC, the existence of these two phases, and the preference of one to the other one in the current explanations of the early universe.
Hartmann352
Between the information contained in these two papers, I've included an explanation of the leading paper from physics.org.
When we discuss the Big Bang vs. the infinite steady state theories, I think that these papers, of the many to be found on this topic, offer the most easily understood with the most robust mathematical and physical framework.
This is not to say that I completely agree with the steady state of an infinite age theory, because I've been in agreement with Einstein's theories.
Higher mathematics combined with a greater ability to provide data to be crunched from ever more complicated and far more effective gathering of the electromagnetic spectrum from improved orbital, ground stationary and now, with the JWST located at Lagrange Point 2, may yet yield the incontrovertible evidence needed to either overthrow Einstein and his theories or further enshrine them. And, they may also yield results falling somewhere in the middle ground.
Cosmology from quantum potential
by Ahmed Farag Ali 1,2 ∗ and Saurya Das 3 †
1. Center for Theoretical Physics,
Zewail City of Science and Technology, Giza, 12588, Egypt.
2. Dept. of Physics, Faculty of Sciences, Benha University, Benha, 13518, Egypt. and
3. Department of Physics and Astronomy, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta, Canada T1K 3M4
It was shown recently that replacing classical geodesics with quantal (Bohmian) trajectories gives rise to a quantum corrected Raychaudhuri equation (QRE). In this article we derive the second order Friedmann equations from the QRE, and show that this also contains a couple of quantum correction terms, the first of which can be interpreted as cosmological constant (and gives a correct estimate of its observed value), while the second as a radiation term in the early universe, which gets rid of the big-bang singularity and predicts an infinite age of our universe.
The generally accepted view of our universe (homogeneous, isotropic, spatially flat, obeying general relativity, and currently consisting of about 72% Dark Energy, likely in the form of a cosmological constant Λ, about 23% Dark Matter, and the rest observable matter), implies its small acceleration, as inferred from Type IA supernova observations, CMBR data and baryon acoustic oscillations. However, quite a few things remain to be better understood, e.g.:
(i) the smallness of Λ, about 10−123 in Planck units (‘the smallness problem’),
(ii) the approximate equality of vacuum and matter density in the current epoch (‘the coincidence problem’),
(iii) the apparent extreme fine-tuning required in the early universe, to have a spatially flat universe in the current epoch (‘the flatness problem’),
(iv) the true nature of dark matter, and
(v) the beginning of our universe, or the so-called big- bang.
In summary, we have shown here that as for the QRE, the second order Friedmann equation derived from the QRE also contains two quantum correction terms. These terms are generic and unavoidable and follow naturally in a quantum mechanical description of our universe. Of these, the first can be interpreted as cosmological con- stant or dark energy of the correct (observed) magnitude and a small mass of the graviton (or axion). The second quantum correction term pushes back the time singu- larity indefinitely, and predicts an everlasting universe. While inhomogeneous or anisotropic perturbations are not expected to significantly affect these results, it would be useful to redo the current study with such small per- turbations to rigorously confirm that this is indeed the case. Also, as noted in the introduction, we assume it to follow general relativity, whereas the Einstein equations may themselves undergo quantum corrections, especially at early epochs, further affecting predictions. Given the robust set of starting assumptions, we expect our main results to continue to hold even if and when a fully satis- factory theory of quantum gravity is formulated. For the cosmological constant problem at late times on the other hand, quantum gravity effects are practically absent and can be safely ignored. We hope to report on these and related issues elsewhere.
See: https://arxiv.org/pdf/1404.3093v3.pdf
No Big Bang? Quantum equation predicts universe has no beginning
by Lisa Zyga , Phys.org
February 9, 2015

This is an artist's concept of the metric expansion of space, where space (including hypothetical non-observable portions of the universe) is represented at each time by the circular sections. Note on the left the dramatic expansion (not to scale) occurring in the inflationary epoch, and at the center the expansion acceleration. The scheme is decorated with WMAP images on the left and with the representation of stars at the appropriate level of development. Credit: NASA
The universe may have existed forever, according to a new model that applies quantum correction terms to complement Einstein's theory of general relativity. The model may also account for dark matter and dark energy, resolving multiple problems at once.
The widely accepted age of the universe, as estimated by general relativity, is 13.8 billion years. In the beginning, everything in existence is thought to have occupied a single infinitely dense point, or singularity. Only after this point began to expand in a "Big Bang" did the universe officially begin.
Although the Big Bang singularity arises directly and unavoidably from the mathematics of general relativity, some scientists see it as problematic because the math can explain only what happened immediately after—not at or before—the theorized singularity.
"The Big Bang singularity is the most serious problem of general relativity because the laws of physics appear to break down there," Ahmed Farag Ali at Benha University and the Zewail City of Science and Technology, both in Egypt, told Phys.org.
Ali and coauthor Saurya Das at the University of Lethbridge in Alberta, Canada, have shown in a paper published in Physics Letters B that the Big Bang singularity can be resolved by their new model in which the universe has no beginning and no end.
Old ideas revisited
The physicists emphasize that their quantum correction terms are not applied ad hoc in an attempt to specifically eliminate the Big Bang singularity. Their work is based on ideas by the theoretical physicist David Bohm, who is also known for his contributions to the philosophy of physics. Starting in the 1950s, Bohm explored replacing classical geodesics (the shortest path between two points on a curved surface) with quantum trajectories.
In their paper, Ali and Das applied these Bohmian trajectories to an equation developed in the 1950s by physicist Amal Kumar Raychaudhuri at Presidency University in Kolkata, India. Raychaudhuri was also Das's teacher when he was an undergraduate student of that institution in the '90s.
Using the quantum-corrected Raychaudhuri equation, Ali and Das derived quantum-corrected Friedmann equations, which describe the expansion and evolution of universe (including the Big Bang) within the context of general relativity. Although it's not a true theory of quantum gravity, the model does contain elements from both quantum theory and general relativity. Ali and Das also expect their results to hold even if and when a full theory of quantum gravity is formulated.
No singularities nor dark stuff
In addition to not predicting a Big Bang singularity, the new model does not predict a "big crunch" singularity, either. In general relativity, one possible fate of the universe is that it starts to shrink until it collapses in on itself in a big crunch and becomes an infinitely dense point once again.
Ali and Das explain in their paper that their model avoids singularities because of a key difference between classical geodesics and Bohmian trajectories. Classical geodesics eventually cross each other, and the points at which they converge are singularities. In contrast, Bohmian trajectories never cross each other, so singularities do not appear in the equations.
In cosmological terms, the scientists explain that the quantum corrections can be thought of as a cosmological constant term (without the need for dark energy) and a radiation term. These terms keep the universe at a finite size, and therefore give it an infinite age. The terms also make predictions that agree closely with current observations of the cosmological constant and density of the universe.
New gravity particle
In physical terms, the model describes the universe as being filled with a quantum fluid. The scientists propose that this fluid might be composed of gravitons—hypothetical massless particles that mediate the force of gravity. If they exist, gravitons are thought to play a key role in a theory of quantum gravity.
In a related paper, Das and another collaborator, Rajat Bhaduri of McMaster University, Canada, have lent further credence to this model. They show that gravitons can form a Bose-Einstein condensate (named after Einstein and another Indian physicist, Satyendranath Bose) at temperatures that were present in the universe at all epochs.
Motivated by the model's potential to resolve the Big Bang singularity and account for dark matter and dark energy, the physicists plan to analyze their model more rigorously in the future. Their future work includes redoing their study while taking into account small inhomogeneous and anisotropic perturbations, but they do not expect small perturbations to significantly affect the results.
"It is satisfying to note that such straightforward corrections can potentially resolve so many issues at once," Das said.
See: https://phys.org/news/2015-02-big-quantum-equation-universe.html
Dark matter and dark energy from Bose-Einstein condensate
March 25, 2015
by Saurya Das 1∗ and Rajat K. Bhaduri2†
1. Department of Physics and Astronomy, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta, Canada T1K 3M4
2. Department of Physics and Astronomy, McMaster University, Hamilton, Ontario, Canada L8S 4M1
We show that Dark Matter consisting of bosons of mass of about 1 eV or less has critical tem- perature exceeding the temperature of the universe at all times, and hence would have formed a Bose-Einstein condensate at very early epochs. We also show that the wavefunction of this condensate, via the quantum potential it produces, gives rise to a cosmological constant which may account for the correct dark energy content of our universe. We argue that massive gravitons or axions are viable candidates for these constituents. In the far future this condensate is all that remains of our universe.
In this paper we show that if dark matter (DM) is assumed to consist of a gas of bosons of mass m, then for m ≤ 1eV , the critical temperature below which they will form a Bose-Einstein condensate (BEC) exceeds the temperature of the universe at all times. Therefore they would form such a condensate at very early epochs, in which a macroscopic fraction of the bosons fall to the ground state with little or no momentum and zero pressure, and therefore may be considered as viable candidates for cold dark matter (CDM). Further, via the quantum po- tential that it produces, the macroscopic wavefunction of the condensate gives rise to a positive cosmological constant in the Friedmann equation, whose magnitude depends on m, and for m ≃ 10−32 eV , one obtains the observed value of the cosmological constant. Therefore bosons with this tiny mass can account for both DM and dark energy (DE) in our universe. We argue that massive gravitons or axions are viable candidates for these bosons. Finally we speculate on the ultimate fate of our universe, and end with some open problems.
In summary, we have shown here that bosons of tiny mass should form a Bose-Einstein condensate (BEC) at early times and may account for the DM content of the universe, while its macro- scopic wavefunction can account for the DE. Both mas- sive gravitons and axions are viable candidates of bosons of this mass, and hence that of DM and DE. While the former requires a modification of general relativity, the latter requires extension of the standard model.
While this picture predicts a high degree of homogeneity and isotropy at large scales (as observed), it still allows for relatively small variations of densities, temperatures etc. at smaller scales. It will be interesting to investigate other testable predictions of this BEC, such as its heat capacity, the distribution of DM, response to galaxy ro- tations etc. We hope to report on these elsewhere.

FIG. 1: NB and NR vs. T. .
Note added
In this note we list features of previous works in BEC in the context of cosmology. In [9], the authors use the same formula for Tc as our Eq.(1), and conjectured that the infinite heat conductivity of the BEC may account for the uniform microwave background temperature. In [10], it was proposed that the BEC manifests itself as DE and DM at different epochs. In [11], DM candidate of a BEC formed out of the ‘phion’ field in modified gravity was considered. In [12], a cold star composed of a dilute BEC was studied. In [13], [16], [17], [18], [20] and [21], properties of various forms of BEC DM were studied. In [14] and [24], the possibility of axions as a BEC was examined. Background geometries and black holes made up of BEC were considered in [15]. DM composed of a BEC of particles obeying infinite statistics was studied in [19]. In [22] BEC in loop quantum cosmology was studied. In [23] it was shown that DM can be well approximated by BEC at large scales, although their estimate of boson mass was higher than that proposed in this paper.
See: https://arxiv.org/pdf/1411.0753.pdf
Bose-Einstein condensate in cosmology
August 30, 2018
Saurya Das (U. Lethbridge), R. K. Bhaduri (McMaster U.)
Two of the enduring mysteries in cosmology are darkApplying the seminal work of Bose in 1924 on what was later known as Bose-Einstein statistics, Einstein predicted in 1925 that at sufficiently low temperatures, a macroscopic fraction of constituents of a gas of bosons will drop down to the lowest available energy state, forming a `giant molecule' or a Bose-Einstein condensate (BEC), described by a `macroscopic wavefunction'. In this article we show that when the BEC of ultralight bosons extends over cosmological length scales, it can potentially explain the origins of both dark matter and dark energy. We speculate on the nature of these bosons.
matter (DM) and dark energy (DE). Whereas DM holds
the rotating galaxies together, DE makes the expanding
universe accelerate. In accounting for the distribution
of mass/energy in the universe, visible hadronic matter
and radiation contribute only about five percent, DM
about twenty five percent, while the rest, a whopping
seventy percent, comes from DE . To start with, the constituents of DE are not known, despite viable candidates such as the cosmological constant and a dynamical scalar field. The constituents of DM are not known either. There has been many studies invoking weakly in- teracting massive particles (WIMPs) that may form cold DM. Not only does it have shortcomings in reproducing the DM density profiles within a galaxy, no such particle has been experimentally found. Other DM candidates include solitons, massive compact (halo) objects, primordial black holes, gravitons etc. They have similar shortcomings.
Given that DM is all-pervading, cold and dark, and clumped near galaxies, we pose the following question: can it be a giant BEC, of cosmological length scales? Following the paper by Bose which laid the foundations of Bose-Einstein statistics [9], Einstein predicted that a gas of bosons will form a BEC at sufficiently low tem- peratures [10]. Here we show that following an earlier proposal by the current authors:
(i) a sea of weakly interacting light bosons can form a BEC, preserving large scale homogeneity and isotropy, and be a viable DM candidate, as long as the mass of each constituent does not exceed a few eV/c2 2, and
(ii) the quantum potential associated with the above BEC can also explain DE.
Note that in a BEC, the bosons are in the lowest energy state that is nearly at zero energy, even if outside the condensate the bosons are highly relativistic due to its low mass. We should point out that BEC model for DM has been studied by many authors in the past. For example, one can consider a scalar field dark matter (SFDM) that invokes spin zero ultralight bosons whose Compton wave length spans cosmic distances. But as mentioned earlier, the novel aspect of our model is that it also provides us with a viable source of DE. In this semi-technical article, we present the bulk of our work in an elementary fashion using Newtonian dynamics, after staging the backdrop of the cosmological model.
There has been many studies invoking weakly in- teracting massive particles (WIMPs) that may form cold DM. Not only does it have shortcomings in reproducing the DM density profiles within a galaxy, no such par- ticle has been experimentally found. Other DM candidates include solitons, massive compact (halo) objects, primordial black holes, gravitons etc. They have similar shortcomings.
Given that DM is all-pervading, cold and dark, and clumped near galaxies, we pose the following question: can it be a giant BEC, of cosmological length scales? Following the paper by Bose which laid the foundations of Bose-Einstein statistics, Einstein predicted that a gas of bosons will form a BEC at sufficiently low temperatures.
See: https://arxiv.org/pdf/1808.10505.pdf
See: https://link.springer.com/article/10.1140/epjc/s10052-016-4182-x
When you consider a universe following the standard Einstein cosmology, the dynamics of the universe is described by Einstein's general relativity equations, one can see that there exists a mysterious singularity at the beginning of time, the so-called big bang. This singularity may be considered as a deficiency of Einstein cosmology at high energies. Actually, you may assert that the big bang implies the breakdown of general relativity at scales with high energies, whereas we know from the observational evidence, such as the existence of the cosmic microwave background, that the big bang model works at scales lower than Planck energy scale. At these scales, the universe was full of a hot photon–baryon combination almost described as a radiation fluid. This hot combination was cooling down as the universe was experiencing the expansion, and due to the different scaling behaviors of pure radiation and pure matter, the energy density of non-relativistic matter started to dominate over the energy density of radiation and led to the formation of structures, which we see today as the galactic filaments and the cosmic web.
In the Bose–Einstein Condensation (BEC) model, the dark matter can be described as a non-relativistic Newtonian gravitational condensate, whose pressure and energy density are related by a barotropic equation of state. Based on the above arguments, we assume the possibility that the Bose–Einstein condensation might have happened during the early stages of cosmological evolution of the universe with a temperature comparable to the critical temperature for Bose–Einstein condensation, where m is the particle mass, n is the particle density, and 𝑘BkB is Boltzmann’s constant.
If you assume there are two phases of dark matter, one as the bosonic particles before BEC, and the other one as BEC dark matter, you might ask: “is there any experimental indication for the occurrence of BEC, the existence of these two phases, and the preference of one to the other one?” and “why is it necessary to distinguish ordinary dark matter from BEC dark matter?” Of course, at present there is no direct evidence for the occurrence of BEC, the existence of these two phases, and the preference of one to the other one in the current explanations of the early universe.
Hartmann352

