What does this motion tell us about the Earth's motion in space? If you ever had a spinning top, you know that its axis tends to stay lined up in the same direction--usually, vertically, though in space any direction qualifies.
|
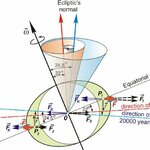
| Precession of a spinning
top: the spin axis traces
the surface of a cone. |
Give it a nudge, however, and the axis will start gyrating wildly around the vertical, its motion tracing a cone (drawing above).
The spinning Earth moves like that, too, though the time scale is much slower--each spin lasts one day, but each gyration around the cone takes 26 000 years. The axis of the cone is perpendicular to the plane of the ecliptic.
The cause of the precession is the equatorial bulge of the Earth, caused by the centrifugal force of the Earth's rotation (the centrifugal force is discussed in a later section). That rotation changes the Earth from a perfect sphere to a slightly flattened one, thicker across the equator. The attraction of the Moon and Sun on the bulge is then the "nudge" which makes the Earth precess.
Through each 26 000-year cycle, the direction in the sky to which the axis points goes around a big circle, the radius of which covers an angle of about 23.5°. The pole star to which the axis points now (within about one degree) used to be distant from the pole, and will be so again in a few thousand years (for your information, the closest approach is in 2017). Indeed, the "pole star" used by ancient Greek sailors was a different one, not nearly as close to the celestial pole.
Because of the discovery mady by Hipparchus, the word "precession" itself no longer means "shift forward" but is now applied to any motion of a spin axis around a cone--for instance, the precession of a gyroscope in an airplane's instrument, or the precession of a spinning satellite in space.
Precession of a spinning scientific payload (also known as its "coning"--from "cone"--or its "nutation") is an unwelcome feature, because it complicates the tracking of its instruments. To eliminate it, such satellites use "nutation dampers," small tubes partially filled with mercury. If the satellite spins as it was designed to do, the mercury merely flows to the part of the tube most distant from the spin axis, and stays there. However, if the axis of rotation precesses, the mercury sloshes back and forth in the tube. Its friction then consumes energy, and since the source of the sloshing is the precession of the spin axis, that precession (very gradually) loses energy and dies down.
- [In the section on the calendar, we saw that the Earth's rotation is slowed down very gradually by the tides, raised by the gravity of the Moon. That process is a bit similar to the action of nutation dampers: the energy of the tides is "lost"--that is, converted to heat--when the waves caused by tides break up on the seashore, and that loss is ultimately taken away from the rotational motion (not the precession) of the Earth]
As already noted, the Earth's orbit is not perfectly round, but is slightly elongated. The Earth therefore comes closest to the Sun in the first week of January (the exact day varies a little). It means that just when the northern hemisphere experiences winter and receives the least amount of sunlight, the Earth as a whole receives the most (the swing is about 3%, peak to peak). This makes northern winters milder, and northern summers are milder too, since they occur when the Earth is most distant from the Sun.
The opposite is true south of the equator: the beginning of January occurs there in summer, and therefore one expects southern summers to be hotter, and southern winters colder, than those north of the equator. This effect is however greatly weakened, because by far most of the the southern hemisphere is covered by ocean, and the water tempers and moderates the climate. |
| Right now, northern winter occurs in the part of the Earth's orbit where the north end of the axis points away from the Sun. However, since the axis moves around a cone, 13,000 years from now, in this part of the orbit, it will point towards the Sun, putting it in mid-summer just when the Earth is closest to the Sun. |

See: https://www.researchgate.net/figure/Precession-Period-for-the-Planets-and-Moon_tbl3_335313110
At that time one expects northern climate to be more extreme, and the oceans then have a much smaller effect, since the proportion of land in the northern hemisphere is much larger. Milankovich argued that because winters were colder, more snow fell, feeding the giant glaciers. Furthermore, he said, since snow was white, it reflected sunlight, and with more severe winters, the snow-covered land warmed up less effectively once winter had ended. Climate is maintained by a delicate balance between opposing factors, and Milankovich argued that this effect alone was enough to upset that balance and cause ice ages.
Milankovich was aware that this was just one of several factors, since it turns out that ice ages don't recur every 26,000 year, nor do they seem common in other geological epochs. The eccentricity of the Earth's orbit, which determines the closest approach to the Sun, also changes periodically, as does the inclination of the Earth's axis to the ecliptic.
With foregoing in mind, the Earth's precession is 26,000 years. Glance then at the table of precession speeds for the planets in our solar system.
See: https://pwg.gsfc.nasa.gov/stargaze/Sprecess.htm
* Coriolis effect - describes the pattern of deflection taken by objects not firmly connected to the ground as they travel long distances around Earth. The Coriolis effect is responsible for many large-scale weather patterns.
The key to the Coriolis effect lies in Earth’s rotation. Specifically, Earth rotates faster at the Equator than it does at the poles. Earth is wider at the Equator, so to make a rotation in one 24-hour period, equatorial regions race nearly 1,600 kilometers (1,000 miles) per hour. Near the poles, Earth rotates at a sluggish 0.00008 kilometers (0.00005 miles) per hour.
See: https://education.nationalgeographic.org/resource/coriolis-effect
What this article describes is the speed, or the duration of the precession of the body in question. The Earth's precession is known to be some 26,000 years, whereas that of Uranus, which possesses the fastest precession in our solar system, is about 263 days (72% of 365 days/yr). The longest period of precession is Neptune's, which amounts to some 1,870,000 years.
The speed of precession as explained in your article, does not reflect the speed of light, which nothing, Einstein explained, can surpass. In the case you cite, the precession is "10 billion times faster" than any previous precession ever found which, when viewed by the chart showing the precession of the planets in our solar system, could easily be divisible by 10 billion.
Hartmann352 |
|

![[IMAGE:Spinning Top] [IMAGE:Spinning Top]](/proxy.php?image=https%3A%2F%2Fpwg.gsfc.nasa.gov%2Fstargaze%2FSfigs%2FSprecess.gif&hash=2afcde669793e2b67f8d4cfdd0bfce26)
![[IMAGE:Precession of Earth Axis] [IMAGE:Precession of Earth Axis]](/proxy.php?image=https%3A%2F%2Fpwg.gsfc.nasa.gov%2Fstargaze%2FSfigs%2FSpreceq.gif&hash=ad5672453bf0d80c579186b1b563a421)


