What is the highest number before infinity?
- Thread starter Chaman Chopra
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
The one directly before it. Infinity is always increasing. Infinity is one way.....out. Never in.
Infinity isn't actually a number, as you cannot do any math with it. 1+infinity is infinity and infinity -10000000000000000000000000 is still infinity. Therefore, the question doesn't have an answer.
Please Somebody Help me out With this?
Special Properties of Infinity |
|---|
∞ + ∞ = ∞ |
-∞ + -∞ = -∞ |
|
∞ × ∞ = ∞ |
-∞ × -∞ = ∞ |
-∞ × ∞ = -∞ |
|
x + ∞ = ∞ |
x + (-∞) = -∞ |
x - ∞ = -∞ |
x - (-∞) = ∞ |
|
For x>0 : |
x × ∞ = ∞ |
x × (-∞) = -∞ |
For x<0 : |
x × ∞ = -∞ |
x × (-∞) = ∞ |
"Undefined" Operations |
|---|
0 × ∞ |
0 × -∞ |
∞ + -∞ |
∞ - ∞ |
∞ / ∞ |
∞0 |
1∞ |
Simple explanations;
What is Infinity?
Introduction to Sets
Advanced explanations;
Infinity - Wikipedia

Transfinite number - Wikipedia


Continuum hypothesis | mathematics
Continuum hypothesis, statement of set theory that the set of real numbers (the continuum) is in a sense as small as it can be. In 1873 the German mathematician Georg Cantor proved that the continuum is uncountable—that is, the real numbers are a larger infinity than the counting numbers—a key
www.britannica.com

Transfinite number | mathematics
Transfinite number, denotation of the size of an infinite collection of objects. Comparison of certain infinite collections suggests that they have different sizes even though they are all infinite. For example, the sets of integers, rational numbers, and real numbers are all infinite; but each is
www.britannica.com
Fun reading;
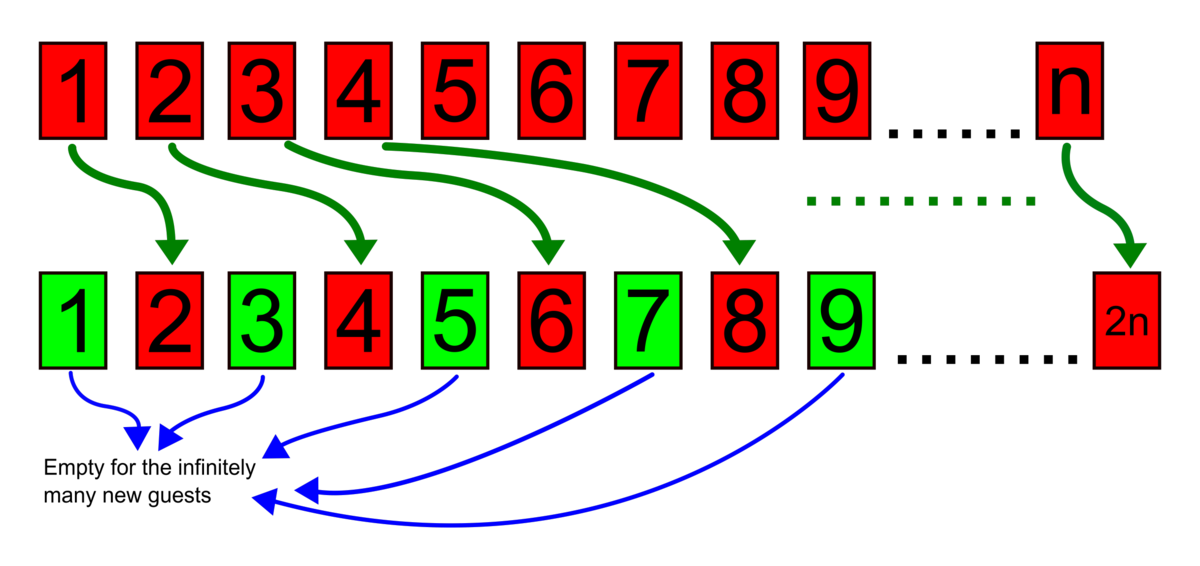
Hilbert's paradox of the Grand Hotel - Wikipedia


Pigeonhole principle - Wikipedia

https://en.wikipedia.org/wiki/Infinite_monkey_theorem
Yeah, pretty much since numbers go infinitely in both directions, positive and negative.Wait, how can you have negative infinity? Counting backwards forever?
efarina96
BANNED
If that were true, then a vector and a line would be the same thing. A vector is essentially infinity in two dimensions with 2 definitive boundaries, its plane and its starting/stopping point. A line is infinity in two dimensions with a single boundary defined by its plane of existence. You are so busy trying to make calculations with infinity it seemingly has never occurred to you to try defining infinity in terms of its relativity.Infinity isn't actually a number, as you cannot do any math with it. 1+infinity is infinity and infinity -10000000000000000000000000 is still infinity. Therefore, the question doesn't have an answer.
The point of this was to show that infinity ins't something you can calculate with, which made the question impossible to answer. I don't quite understand what that means.If that were true, then a vector and a line would be the same thing. A vector is essentially infinity in two dimensions with 2 definitive boundaries, its plane and its starting/stopping point. A line is infinity in two dimensions with a single boundary defined by its plane of existence. You are so busy trying to make calculations with infinity it seemingly has never occurred to you to try defining infinity in terms of its relativity.
efarina96
BANNED
Your point appears to be that quantifications of infi ity in any form are meaningless. 1+infinity is infinity so we might as well stop thinking about it right there, it is what it is right? What is "one"of anything after all? I hold "one" apple in my hands, and attempt to quantify it by saying it is "exactly" 5 inches tall. But then I measure it to the nearest quadrillionth of a quadrillionth of an inch- am I likely to find that my initial measurement was exact, when incorporaring this level of precision? No.. In fact, the reality is that no matter what level of precision I use to describe the height of the apple, there is a further level of precision to be reached that will render my initial measurement inaccurate. In fact, no matter how I attempt to measure the dimensions of said apple, there will always be infinite room to improve the precision of my measurement because the apple itslef along with every other element of reality is a manifestation of relative infinity. And so the universe from the perspective of a single apple can be described as 1+infinity=infinity, this description is hardly meaningless and is heavily dependant upon context i.e. relativityThe point of this was to show that infinity ins't something you can calculate with, which made the question impossible to answer. I don't quite understand what that means.
efarina96
BANNED
"One" is an arbitrary construct we impose upon infinity in order to give meaning to our relative observations of reality. Measure a square to the nearest inch... Measure it to the nearest quadrillionth of in inch... Measure it to the nearest quintillion-googolth of a nanometer... Measure it to the nearest AU or light-year. No matter what you do you will find that there is infinite room to improve the precision of your measurement, because reality is infinity and everything is relative.Infinity minus one. So that is still an infinity
Similar threads
- Replies
- 0
- Views
- 90
- Replies
- 1
- Views
- 240
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 2K
TRENDING THREADS
-
What is a living individual and is it naturally universally mobile?
- Started by tonylang
- Replies: 138
-
-
50-foot 'king of the serpents' may have been the biggest snake to ever live
- Started by admin
- Replies: 0

Live Science is part of Future plc, an international media group and leading digital publisher. Visit our corporate site.
© Future Publishing Limited Quay House, The Ambury, Bath BA1 1UA. All rights reserved. England and Wales company registration number 2008885.
