John369
You have certainly picked a series of complicated questions for further elucidation.
Your #1 is especially so.
A field theory formulation of two-time physics in d + 2 dimensions is obtained from the covariant quantization of the constraint system associated with the OSp(n|2) worldline gauge symmetries of two-time physics. Interactions among fields can then be included consistently with the underlying gauge symmetries. Through this process a relation between Dirac’s work in 1936* on conformal symmetry in field theory and the more recent worldline formulation of two-time physics is established while providing a worldline gauge symmetry basis for the field equations in d + 2 dimensions. It is shown that the field theory formalism goes well beyond Dirac’s goal of linearizing conformal symmetry. In accord with recent results in the worldline approach of two-time physics, the d + 2 field theory can be brought down to diverse d dimensional field theories by solving the subset of field equations that correspond to the “kinematic” constraints. This process embeds the one “time” in d-dimensions in different ways inside the d + 2 dimensional spacetime. Thus, the two-time d + 2 field theory appears as a more fundamental theory from which many one-time d dimensional field theories are derived. It is suggested that the hidden symmetries and relations among computed quantities in certain d-dimensional interacting field theories can be taken as the evidence for the presence of a higher unifying structure in a d + 2 dimensional spacetime. These phenomena have similarities with ideas such as dualities, AdS-CFT correspondence and holography.
* In 1936 Paul Adrien Maurice Dirac OM FRS invented a field theory approach for rewriting conformal field theory in four dimensions in a manifestly SO(4,2) covariant form in six dimensions. Dirac’s fields Φ(X) depend on 6 coordinates XM which have two timelike dimensions, just like the dynamical coordinates XM (τ, · · ·) used in the formalism of two-time physics on the worldline or worldvolume.
Dirac’s goal was to realize conformal symmetry linearly in 4+2 dimensional field theory, and this remained the primary motivation for the work in the literature that followed his paper. The goals and results of two-time physics lie in more general directions, although conformal symmetry is included as a special outcome in a particular gauge. In two-time physics there is an underlying new gauge principle that is responsible for recasting the d + 2 dimensional theory as many possible d-dimensional theories. The purpose of the present paper is twofold. First, to establish the relationship between the gauge principles in two time physics on the worldline and Dirac’s approach in field theory; second, to demonstrate directly in field theory that diverse one-time field theories emerge in d dimensions from the same field equations in d + 2 dimensions. It will be seen that the path of derivation of d dimensional field theories is in precise correspondence with making gauge choices in the worldline theory, the important step being the embedding of the time coordinate in d dimensions in various ways inside the d + 2 dimensions. In this way one can see that the d + 2 dimensional two-time theory plays a unifying role in a new sense, including interactions.
Two-time physics in d + 2 dimensions was developed independently in the worldline (and worldvolume) formulation, unaware of the field theory formalism invented by Dirac
permitted the free exploration and development of new insights in the worldline formulation.
See:
https://arxiv.org/pdf/hep-th/0003100.pdf

Historically, the motivation for two-time physics came from duality, and signals for two-timelike dimensions in M-theory** and its extended superalgebra including D-branes***. In particular certain dynamical attempts to try to understand these phenomena directly paved the way to the formalism found in the Sp(2,R) gauge theory. Two-time physics introduced a new gauge principle - Sp(2, R) in phase space, and its generalizations - that insures unitarity, causality and absence of ghosts. This takes care of problems that naively would have arisen in a spacetime with two-timelike dimensions. Morally speaking, this gauge symmetry is related to duality in a generalized sense. The new phenomenon in two-time physics is that this gauge symmetry can be used to obtain various one-time dynamical systems in d dimensions from the same two-time action in d + 2 dimensions, through gauge fixing, thus uncovering a new layer of unification through higher dimensions.
For the complete breakdown, see:
https://arxiv.org/pdf/hep-th/0003100.pdf
** M-Theory - is the name for a unified version of string theory, proposed in in the spring of 1995 at a physics conference on string theory, held at the University of Southern California, by the physicist Edward Witten. At the time of the proposal, there were 5 variations of string theory, but Witten put forth the idea that each was a manifestation of a single underlying theory.
*** D-branes represent a key theoretical tool in the understanding of strongly coupled superstring theory and M-theory. They have led to many striking discoveries, including the precise microphysics underlying the thermodynamic behaviour of certain black holes, and remarkable holographic dualities between large-N gauge theories and gravity.
D-branes are a special and important subset of branes defined by the condition that fundamental strings can end on the D-branes. This is literally the technical definition of D-branes and it turns out that this simple fact determines all of the properties of D-branes.
Perturbatively, fundamental strings are more fundamental than branes or any other objects. In that old-fashioned description, D-branes are "solitons" - configurations of classical fields that arise from the closed strings. They are analogous to magnetic monopoles - which may also be written as classical configurations of the "more fundamental fields" in field theory. In a similar way, D-branes' masses diverge for 𝑔→0g→0.
Non-perturbatively, D-branes and other branes are equally fundamental as strings. In fact, when 𝑔gis sent to infinity, some D-branes may become the lightest objects - usually strings of a dual (S-dual) theory.
See:
https://physics.stackexchange.com/questions/4988/what-is-a-d-brane
However, your #2, is much easier to understand.
In flat spacetime, there is an analog of the Pythagorean theorem. It is called the interval, and its equation is, in analogy with the Pythagorean one,
where c is the speed of light. It calculates a specific kind of distance between two events: one at time
and position
and another at time
at position
.
You’ll have to believe that the curvature of spacetime depends on how “wrong” this interval is, in the same way curvature of surfaces depended on how “wrong” the Pythagorean theorem was. On the other hand, the structure of light cones depends on the exact form of the interval, and so their shape will change whenever curvature is present.
We understand that light cones at a given event (for flat spacetime): just turn on a flashlight, and mark the instant of time the light rays reach each position in space. Our light cones were then something like this:
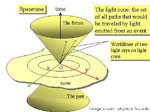
The light cones play a similar role in curved spacetime as does the Pythagorean theorem: locally they are exactly like the one above, but globally, they can have a very different structure. To see this, we first draw the causal strucutre, that is, the set of all light cones, in flat spacetime:

For simplicity, we show the light cones for a given value of time, at some random positions. You must imagine this pattern being repeated for every point in spacetime. Also, we show an example of a time like word line, that is, the trajectory in space and time of a realistic individual, with some of the light cones present in this world line. But let it be clear: every point, every event in spacetime has an associated light cone. We just can’t draw them all because they are nearly infinite in number.
However, everything changes when we finally go to curved spacetime. Let’s show a first example, known as the Van Stockum spacetime
:
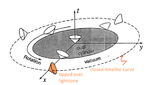
There is – there always is – a drawback. The Van Stockum spacetime is not physically possible, albeit being mathematically possible. What does “possible” mean?
We see that “possible” means “a solution of Einstein’s equations for general relativity”, with the constraints that it respects certain properties of matter and energy that the Van Stockum spacetime does not.
In spacetime, there is a distance (called the interval) which is an analog of Pythagora’s formula. As the latter, it is only correct in flat spaces, but can also be defined locally in every event in spacetime – this is how one has light cones around every event. When spacetime is curved, the interval’s real expression changes, and with that, the structure of the light cones. This allows for tipping over of the light cones, which in turn allows for closed curves which are everywhere timelike. An observer in such a worldline would see himself going to the future at every instant, and then would realize he went back in time – in the same way you may try going straight North from the Equator, keep walking, then find yourself at the South Pole in the end.
See:
https://forums.livescience.com/threads/two-time-physics-questions.4913/
See:
https://www.thoughtco.com/is-time-travel-possible-2699431
See:
https://arxiv.org/pdf/gr-qc/9707021.pdf
I hope this helps you grasp these two aspects of the whole you have tossed out for discussion.
Hartmann352




