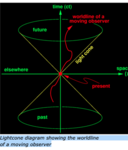
Light travels at the same speed for all reference frames due to Einstein's theory of relativity. The light would travel away from the fast object at the speed of light to the reference frame of the speeding object, but you would also see the light traveling at the speed of light from a nonmoving reference frame.
Instead, you are having trouble with the invariance of the speed of light, you might prefer an approach that does not use it. It turns out that, if you use only the principle of relativity, you can prove that there are two possibilities. Either there is no finite invariant speed, in which case you get Galilean relativity, or there is a finite invariant speed, in which case you get special relativity. Then it becomes a simple matter of experimentally testing to see which of the two possibilities corresponds to reality.
If you really wanted to derive the invariance of c from time dilation, length contraction, and the relativity of simultaneity, the procedure is straight forward. Time dilation, length contraction, and the relativity of simultaneity together give you the Lorentz transform:
𝑡′=𝛾𝑡−𝛾𝑣𝑥/𝑐2t′=γt−γvx/c2
𝑥′=𝛾𝑥−𝛾𝑣𝑡x′=γx−γvt
Then a light pulse in the unprimed frame is given by
𝑥=𝑐𝑡x=ct
so substituting in we get the equation for a light pulse in the unprimed frame
𝑡′=𝛾𝑡−𝛾𝑣𝑡/𝑐t′=γt−γvt/c
𝑥′=𝛾𝑐𝑡−𝛾𝑣𝑡=𝑐𝑡′x′=γct−γvt=ct′
So the speed of the light pulse is c in the primed frame also. The speed of light is therefore invariant.
Let's examine some history.
Isaac Newton pursued a more philosophical vein. Colours, he insisted, lie not in the medium and not in objects but in light rays—and since colours are qualities, the rays themselves must be made of a material substance. Claiming that his account would undoubtedly stimulate further research, Newton thoughtfully provides full instructions, including dimensions, for an experimental set-up that he had designed to demonstrate—not test—the validity of his propositions. He recommended passing sunlight first through a prism and then through a lens on to a sheet of paper. By moving the paper backwards and forwards through the focal point, the refracted beam can, he reported, be seen splitting into colours and then reuniting into white light. However, even the incomplete trouble-shooting details he provides confirm how tricky it can be to obtain the desired effects.
Isaac Newton in 1686 postulated these three laws:
- Objects in motion or at rest remain in the same state unless an external force imposes change. This is also known as the concept of inertia.
- The force acting on an object is equal to the mass of the object multiplied by its acceleration. In other words, you can calculate how much force it takes to move objects with various masses at different speeds.
- For every action, there is an equal and opposite reaction.
Recall that at the beginning of the 17th century, the general consensus was that light didn't have a speed, that it just appeared instantaneously, either present or not
During the 1600s this idea was seriously challenged. First, by Dutch scientist
Isaac Beeckman in 1629, who set up a series of mirrors around a gunpowder explosions to see if observers noticed any difference in the when the flashes of light appeared.
Unfortunately for Beeckman and the progress of science, the results were inconclusive, but then in 1676 Danish astronomer
Ole Rømer noticed strange variations in the eclipse times of one of
Jupiter's moons over the course of a year.
Could this be because light took a longer time to travel from Jupiter when Earth was further away? Rømer thought so, and his rough calculations put the speed of light at about 220,000 kilometres per second – not a bad estimate at all, especially considering the data he would have had on planet sizes wasn't all that accurate.
Further experiments with beams of light on our own planet edged scientists closer to the right number, and then in the mid-1800s physicist James Clerk Maxwell introduced
his Maxwell's equations – ways of measuring electric and magnetic fields in a vacuum.
Maxwell's equations fixed the electric and magnetic properties of empty space, and after noting that the speed of a massless electromagnetic radiation wave was very close to the supposed speed of light, Maxwell suggested they might match exactly.
It turns out Maxwell was right, and for the first time we could measure the speed of light based on other constants in the Universe.
At the same time, Maxwell's work strongly suggested that light was itself an electromagnetic wave, and after this idea was confirmed, it got picked up by
Albert Einstein in 1905 as part of his theory of
special relativity.
According to Einstein, in his 1949 book "
Autobiographical Notes(opens in new tab)" (Open Court, 1999, Centennial Edition), the budding physicist began questioning the behavior of light when he was just 16 years old. In a thought experiment as a teenager, he wrote, he imagined chasing a beam of light.
Classical physics would imply that as the imaginary Einstein sped up to catch the light, the light wave would eventually come to a relative speed of zero — the man and the light would be moving at speed together, and he could see light as a frozen
electromagnetic field. But, Einstein wrote, this contradicted work by another scientist, James Clerk Maxwell, whose equations required that electromagnetic waves always move at the same speed in a vacuum: 186,282 miles per second (300,000 kilometers per second).
Philosopher of physics John D. Norton challenged Einstein's story in his book "
Einstein for Everyone" (Nullarbor Press, 2007), in part because as a 16-year-old, Einstein wouldn't yet have encountered Maxwell's equations. But because it appeared in Einstein's own memoir, the anecdote is still widely accepted.
If a person could, theoretically, catch up to a beam of light and see it frozen relative to their own motion, would physics as a whole have to change depending on a person's speed, and their vantage point?
Einstein recounted, he sought a unified theory that would make the rules of physics the same for everyone, everywhere, all the time.
This, wrote the physicist, led to his eventual musings on the theory of special relativity, which he broke down into another thought experiment: A person is standing next to a train track comparing observations of a lightning storm with a person inside the train. And because this is physics, of course, the train is moving nearly the speed of light.
Einstein imagined the train at a point on the track equally between two trees. If a bolt of lightning hit both trees at the same time, the person beside the track would see simultaneous strikes. But because they are moving toward one lightning bolt and away from the other, the person on the train would see the bolt ahead of the train first, and the bolt behind the train later.
Einstein concluded that simultaneity is not absolute, or in other words, that simultaneous events as seen by one observer could occur at different times from the perspective of another. It's not lightspeed that changes, he realized, but time itself that is relative. Time moves differently for objects in motion than for objects at rest. Meanwhile, the speed of light, as observed by anyone anywhere in the universe, moving or not moving, is always the same.
Today the speed of light, or
c as it's commonly known, is considered the cornerstone of
special relativity – unlike space and time, the speed of light is constant, independent of the observer.
What's more, this constant underpins much of what we understand about the Universe. It matches
the speed of a gravitational wave, and yes, it's the same
cthat's in the famous equation E=mc2.
E = mc^2 translates to "energy is equal to mass times the speed of light squared." In other words, wrote
PBS Nova, energy (E) and mass (m) are interchangeable. They are, in fact, just different forms of the same thing.
But they're not easily exchanged. Because the speed of light is already an enormous number, and the equation demands that it be multiplied by itself (or squared) to become even larger, thus a small amount of mass contains a huge amount of energy. For example, PBS Nova explained, "If you could turn every one of the atoms in a paper clip into pure energy — leaving no mass whatsoever — the paper clip would yield [the equivalent energy of] 18 kilotons of TNT. That's roughly the size of the bomb that destroyed Hiroshima in 1945."
We don't just have the word of Maxwell and Einstein for what the speed of light is, though. Scientists have
measured it by bouncing lasers back from objects and
watching the way gravity acts on planets, and all these experiments come up with the same figure.
One of the many implications of Einstein's special relativity work is that time moves relative to the observer. An object in motion experiences time dilation, meaning that when an object is moving very fast it experiences time more slowly than when it is at rest.
When astronaut Scott Kelly spent nearly a year aboard the
International Space Station starting in 2015, he was moving much faster than his twin brother, astronaut Mark Kelly, who spent the year on the planet's surface. Due to time dilation, Mark Kelly
aged just a little faster than Scott — some "five milliseconds," according to the earth-bound twin. Since Scott wasn't moving near lightspeed, the actual difference in aging due to time dilation was negligible. In fact, considering how much stress and radiation the airborne twin experienced aboard the ISS, some would argue Scott Kelly increased his rate of aging.
But at speeds approaching the speed of light, the effects of time dilation could be much more apparent. Imagine a 15-year-old leaves her high school traveling at 99.5% of the speed of light for five years (from the teenage astronaut's perspective). When the 15-year-old got back to Earth, she would have aged those 5 years she spent traveling. Her classmates, however, would be 65 years old — 50 years would have passed on the much slower-moving planet.
We don't currently have the technology to travel anywhere near that speed. But with the precision of modern technology, time dilation does actually affect human engineering.
GPS devices work by calculating a position based on communication with at least three satellites in distant Earth orbits. Those satellites have to keep track of incredibly precise time in order to pinpoint a location on the planet, so they work based on atomic clocks. But because those atomic clocks are on board satellites that are constantly whizzing through space at 8,700 mph (14,000 km/h), special relativity means that they tick an extra 7 microseconds, or 7 millionths of a second, each day, according to American Physical Society publication
Physics Central. In order to maintain pace with Earth clocks, atomic clocks on GPS satellites need to subtract 7 microseconds each day.
With additional effects from general relativity (Einstein's follow-up to special relativity that incorporates gravity), clocks closer to the center of a large gravitational mass like Earth tick more slowly than those farther away. That effect adds microseconds to each day on a GPS atomic clock, so in the end engineers subtract 7 microseconds and add 45 more back on. GPS clocks don't tick over to the next day until they have run a total of 38 microseconds longer than comparable clocks on Earth.
Special relativity and quantum mechanics are two of the most widely accepted models of how our universe works. But special relativity mostly pertains to extremely large distances, speeds and objects, uniting them in a "smooth" model of the universe. Events in special (and general) relativity are continuous and deterministic, wrote Corey Powell for
The Guardian, which means that every action results in a direct, specific and local consequence. That's different from quantum mechanics, Powell continued: quantum physics are "chunky," with events occurring in jumps or "quantum leaps" that have probabilistic outcomes, not definite ones.
Researchers uniting special relativity and quantum mechanics — the smooth and the chunky, the very large and the very small — have come up with fields like relativistic quantum mechanics and, more recently, quantum field theory to better understand subatomic particles and their interactions.
Researchers striving to connect quantum mechanics and general relativity, on the other hand, consider it to be one of the great unsolved problems in physics. For decades, many viewed
string theory to be the most promising area of research into a unified theory of all physics. Now, a host of additional theories exist. For example, one group proposes
space-time loops to link the tiny, chunky quantum world with the wide relativistic universe.
However, the story doesn't quite end there, thanks to
quantum theory, that branch of physics hinting that the Universe might not be quite as constant as we think.
Quantum field theory says that a vacuum is never really empty: it's filled with elementary particles, rapidly popping in and out of existence. These particles create electromagnetic ripples along the way, the hypothesis goes, and could potentially cause variations in the speed of light.
Studies into these ideas
are ongoing, and we don't know for sure one way or the other yet. For now, the speed of light remains the same as it has for centuries, constant and fixed… but watch this space.
Today, the speed of light, or
c as it's commonly known, is considered the cornerstone of
special relativity – unlike space and time, the speed of light is constant, independent of the observer.
What's more, this constant underpins much of what we understand about the Universe. It matches
the speed of a gravitational wave, and yes, it's the same
cthat's in the famous equation E=mc2.
The Lorentz Invariance, named after Dutch physicist Hendrik Lorentz, holds that the laws of physics are the same for observers throughout
the universe, no matter where they are or how fast they're moving.
The Lorentz Invariance is at the heart of special relativity, which predicts, among other things, that the
speed of light in a vacuum is a constant 186,282 miles (299,791 kilometers) per second, whatever the situation.
This speed is indeed constant in all measurements to date, even those made at the highest energy levels that scientists can produce here on Earth with particle accelerators. And it holds at far higher energies as well, the kinds generated by dramatic astrophysical phenomena, a new study reports.
The study team analyzed data gathered by the High Altitude Water Cherenkov (HAWC) observatory, a system of 300 water tanks built on the shoulder of a volcano in the Mexican state of Puebla. Sensitive detectors inside these tanks measure the cascades of particles generated when high-energy gamma-rays strike the molecules in
Earth's atmosphere.
The observatory has detected evidence of photons with energies above 100 teraelectronvolts — about 1 trillion times higher than the energy of visible light — streaming from at least four different astrophysical sources, reports the new study, which was published online Monday (March 30, 2019) in the journal
Physical Review Letters.
That's a big deal, because it shows that even those supremely potent photons did not exceed the universal speed limit. If they had been moving faster than 186,282 miles per second, they would have decayed into lower-energy particles and never reached the water-tank detectors, study team members said.
We don't just have the word of Maxwell, Lorentz and Einstein for what the speed of light is, though. Scientists have
measured it by bouncing lasers back from objects and
watching the way gravity acts on planets, and all these experiments come up with the same figure.
Q
uantum theory hints that the Universe might not be quite as constant as we think.
Quantum field theory says that a vacuum is never really empty: it's filled with energetic virtual elementary particles, rapidly popping in and out of existence. These particles create electromagnetic ripples along the way, the hypothesis goes, and could potentially cause variations in the speed of light.
Studies into these ideas
are ongoing, and we don't know for sure one way or the other yet. F
But for now, the speed of light remains the same as it has for centuries, constant and fixed.
Hartmann352
See:
https://www.sciencealert.com/why-is-the-speed-of-light-the-speed-of-light
See:
https://www.space.com/36273-theory-special-relativity.html