Question tachyonic particle
- Thread starter ZacharyDelRio
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I am no expert but this may be of interest and pertinent to your question.what would the discovery of a tachyonic particle mean for the field of physics?
Tachyons: The Hypothetical Faster-Than-Light Particles in Physics
The story behind and the connection to the Higgs field, time travel, and dark energy
more.......The Higgs field was a tachyonic field before spontaneous symmetry breaking. All theories that involve tachyonic fields are cases of spontaneous symmetry breaking. The Higgs mechanism is an example of spontaneous symmetry breaking and hence also an example of a tachyonic field at the beginning of the Universe. Nov 12, 2019

Tachyons: The Hypothetical Faster-Than-Light Particles in Physics
The story behind and the connection to the Higgs field, time travel, and dark energy
 medium.com
medium.com
Note that when the Higgs particle was teased out of the Higgs field it lasted a few nanoseconds before it decayed into lower energy particles.
Last edited:
I am no expert but this may be of interest and pertinent to your question.
Tachyons: The Hypothetical Faster-Than-Light Particles in Physics
The story behind and the connection to the Higgs field, time travel, and dark energy
more.......
excellent, thank you for the material!.
Tachyons: The Hypothetical Faster-Than-Light Particles in Physics
The story behind and the connection to the Higgs field, time travel, and dark energy
more.......
excellent, thank you for the material!.
Physicists close in on the exceedingly short life of the Higgs boson
Just because scientists have discovered a particle doesn't mean they know all its properties.
1.6 x 10-22 seconds: That, according to theory, is the lifetime of the Higgs boson, one of the most sought-after particles in the subatomic world. This time is so short that tens of trillions of Higgs bosons might live and die before the light from the device you’re using to read this reaches your eyes.
Physicists are zeroing in on this lifetime in the real world. Poring over data from CERN’s Large Hadron Collider (LHC), scientists have narrowed down the Higgs’ lifespan to something around that 1.6 x 10-22 figure. The scientists were able to do so thanks to data from the CMS, one of the LHC’s detectors. Their work is a major advance–and it’s a sign that, nearly a decade after the Higgs boson’s discovery, there is still quite a bit to learn about the particle.
Hey fellas, after 100 yrs of particles, they are still looking for a "mass" particle. What does this tell you? It tells me that our modern science still.....can not discern what "mass" is.
Mass is not an entity, mass is a property of an entity. Charge is not a property of mass, mass is a property of charge. Mass is the amount of field density of a charge particle. A charge has two densities. An electric and magnetic density. One spins inside the other at cross angles. These two cross spinning fields are woven into a balance, and if anything distorts that current state of balance, these two fields will attempt to restore that balance. The two spinning fields will resist any change in that weave of balance. The amount of resistance to the current state of balance, will depend on the density of those spinning fields. This is how "mass" can be adjusted with the density(energy) of the particle.
Don't think of mass as an amount of stuff. The amount of stuff remains constant. It's the state of the density of the stuff, that expresses as mass. The denser the stuff, the harder to disturb.
There are only two particles, a left and a right handed one. That's it. All the rest are dissolving charge fragments.
Mass is not an entity, mass is a property of an entity. Charge is not a property of mass, mass is a property of charge. Mass is the amount of field density of a charge particle. A charge has two densities. An electric and magnetic density. One spins inside the other at cross angles. These two cross spinning fields are woven into a balance, and if anything distorts that current state of balance, these two fields will attempt to restore that balance. The two spinning fields will resist any change in that weave of balance. The amount of resistance to the current state of balance, will depend on the density of those spinning fields. This is how "mass" can be adjusted with the density(energy) of the particle.
Don't think of mass as an amount of stuff. The amount of stuff remains constant. It's the state of the density of the stuff, that expresses as mass. The denser the stuff, the harder to disturb.
There are only two particles, a left and a right handed one. That's it. All the rest are dissolving charge fragments.
Last edited:
Perhaps, Mr DelRio, the following will aid in your understanding of tachyons.
However intelligent a theory is, we need empirical physics proof is a must. That is the basic characteristic of the scientific method used in modern physics.
All matter around us is made of elementary particles, the building blocks of matter. These particles occur in two basic types called quarks and leptons. Each group consists of six particles, which are related in pairs, or “generations”.
The lightest and most stable particles make up the first generation, whereas the heavier and less-stable particles belong to the second and third generations. All stable matter in the universe is made from particles that belong to the first generation; any heavier particles quickly decay to more stable ones. The six quarks are paired in three generations – the “up quark” and the “down quark” form the first generation, followed by the “charm quark” and “strange quark”, then the “top quark” and “bottom (or beauty) quark”. Quarks also come in three different “colours” and only mix in such ways as to form colourless objects. The six leptons are similarly arranged in three generations – the “electron” and the “electron neutrino”, the “muon” and the “muon neutrino”, and the “tau” and the “tau neutrino”. The electron, the muon and the tau all have an electric charge and a sizeable mass, whereas the neutrinos are electrically neutral and have very little mass.
The neutrino is one of the so-called fundamental particles, which means it isn’t made of any smaller pieces, at least that we know of. Neutrinos are members of the same group as the most famous fundamental particle, the electron (which is powering the device you’re reading this on right now). But while electrons have a negative charge, neutrinos have no charge at all.
Neutrinos are also incredibly small and light. They have some mass, but not much. They are the lightest of all the subatomic particles that have mass. They’re also extremely common—in fact, they’re the most abundant massive particle in the universe. Neutrinos come from all kinds of different sources and are often the product of heavy particles turning into lighter ones, a process called “decay.”
Neutrinos were first predicted in 1930, but they weren’t discovered in experiments until 1956, and scientists thought they were massless until even later. While we keep learning more about neutrinos, with new answers come new mysteries. Physicist Enrico Fermi coined the name “neutrino”, which is Italian for “little neutral one.”
Neutrinos are difficult to study. The only ways they interact is through gravity and the weak force, which is, well, weak. This weak force is important only at very short distances, which means tiny neutrinos can skirt through the atoms of massive objects without interacting. Most neutrinos will pass through Earth without interacting at all. To increase the odds of seeing them, scientists build huge detectors and create intense sources of neutrinos.
There are four fundamental forces at work in the universe: the strong force, the weak force, the electromagnetic force, and the gravitational force. They work over different ranges and have different strengths.
Gravity is the weakest but it has an infinite range. The electromagnetic force also has infinite range but it is many times stronger than gravity. The weak and strong forces are effective only over a very short range and dominate only at the level of subatomic particles. Despite its name, the weak force is much stronger than gravity but it is indeed the weakest of the other three. The strong force, as the name suggests, is the strongest of all four fundamental interactions.
Three of the fundamental forces result from the exchange of force-carrier particles, which belong to a broader group called “bosons”. Particles of matter transfer discrete amounts of energy by exchanging bosons with each other. Each fundamental force has its own corresponding boson – the strong force is carried by the “gluon”, the electromagnetic force is carried by the “photon”, and the “W and Z bosons” are responsible for the weak force. Although not yet found, the “graviton” should be the corresponding force-carrying particle of gravity.
The Standard Model includes the electromagnetic, strong and weak forces and all their carrier particles, and explains well how these forces act on all of the matter particles. However, the most familiar force in our everyday lives, gravity, is not part of the Standard Model, as fitting gravity comfortably into this framework has proved to be a difficult challenge.
The quantum theory used to describe the micro world, and the general theory of relativity used to describe the macro world, are difficult to fit into a single framework. No one has managed to make the two mathematically compatible in the context of the Standard Model. But luckily for particle physics, when it comes to the minuscule scale of particles, the effect of gravity is so weak as to be negligible. Only when matter is in bulk, at the scale of the human body or of the planets for example, does the effect of gravity dominate. So the Standard Model still works well despite its reluctant exclusion of one of the fundamental forces.
Currently, tachyons do not have any current experimental proof. Theoretically tachyons lead to several paradoxes, to the extent that this universe we live in cannot exist if tachyons exist.
The type of universe/universes supporting the existence of tachyons is not currently describable just as every mathematical basis of such universes has not yet been realized. Several non visualizable phenomena including hyper dimensional spaces with mathematical schemes exist and they are often very useful for formulation of visualizable dynamics, too.
Investigate the following for our further edification:
(i) Minkowsky 4 dimensional space-time continuum used to explain special relativistic kinematics and mechanics,
(ii) Riemann space mathematics used by Einstein to obtain the most general (so far) theory of gravity, rectifying Newton’s inverse square law (Newton assumed gravity as instantaneously acting force between any two objects, regardless of their distance of separation, whereas Einstein discovered no interactive force propagates faster than light, due to which there were paradoxes ( Einstein discovered gravity is not a force, but a space-time {nonvisualizable, again} curvature proportional to the mass of the object) with objects gravitationally interacting, while having them separated by such distances that the light takes milli seconds/seconds or minutes/hours as in solar system itself).
Another paper concerning Riemann space and tachyons is 'ON THE RIEMANN HYPOTHESIS AND TACHYONS IN DUAL STRING SCATTERING AMPLITUDES' by Carlos Castro from the Center for Theoretical Studies of Physical Systems Clark Atlanta University, Atlanta, GA, USA
(See: https://vixra.org/pdf/0908.0088v1.pdf )
Castro, in the paper above, explains that "The physical relevance of tachyonic resonances/tachyonic-condensates in bosonic string theory, establishes an important connection between string theory and the Riemann Hypothesis. In addition, one has also a geometrical interpretation of the zeta zeros in the critical line in terms of very special (degenerate) triangular configurations in the upper-part of the complex plane."
(iii) Hilbert space useful in quantum mechanics.
I also suggest that you read Moses Fayngold's book 'Special Relativity and Motion Faster than Light' which covers the ideas about superluminal speeds and special relativity and what happens in theory when objects travel at speeds faster-than-light. Fayngold shows that in all these cases subtle forces of nature conspire to prevent these motions being harnessed to send signals faster than the speed of light.
However, one version of the Standard Model, the string theory with 23 dimensions, supports the existence of tachyons. No other theory includes that possibility, nor is there any evidence.
If you read the Feynman lectures, he does mention that the complete solution of all possible paths for a particle-particle interaction must include particles traveling backwards in time. Reversal of the time direction is not that controversial.
Causality is more than a convenience. Acausal phenomena are extremely hard to either study or contemplate. Like miracles, they just happen. However, the current idea of causality, modified by what happens at the event horizon of a black hole, is pretty far from the simple Aristotelean chain of events. Among other “sacred” ideas, classical causality is already a victim of quantum logic.
All this is preamble to the method to detect a tachyon. They would appear to be acausal. They probably would appear to be traveling backwards in time, which is almost the same as being acausal.
It is assumed that among the tachyons would be at least some with a coefficient of interaction (collision cross-section) that allowed them to be detected in a modern particle chamber, whether they are charged or neutral. I also assume that in such a detector the means of detection involves a collision or other intimate reaction that stops a tachyon. It then converts to a normal particle that registers as an event.
Particle detectors have coincidence detectors that make sure the detected particles come from the beam, and not from incident cosmic rays. Any non-causal event will be filtered out by the coincidence detectors. But those are exactly the kind of events that mark tachyons!
On 4 July 2012, the ATLAS and CMS experiments at CERN's Large Hadron Collider (LHC) announced they had each observed a new particle in the mass region around 126 GeV. This particle is consistent with the Higgs boson but it will take further work to determine whether or not it is the Higgs boson predicted by the Standard Model. The Higgs boson, as proposed within the Standard Model, is the simplest manifestation of the Brout-Englert-Higgs mechanism*. Other types of Higgs bosons are predicted by other theories that go beyond the Standard Model.
We want events that would be filtered out by the coincidence detectors because they do not seem to originate from the beam. Perhaps they really do, but as tachyons, their origin is masked. They just happen. We also want to ignore cosmic ray events.
Tachyon energies are are lower at higher speeds. The closer a tachyon moves to the speed of light, the more mass-energy it has. Given the usual thermal equilibrium of energy in the accelerator’s beam (big assumption here for tachyons) most tachyons will have the same energy as most of that kind of particle. When the tachyon converts to a regular particle, that will be the its contributed mass-energy. Perhaps we can just eliminate events above and below a certain beam energy level.
So we are looking for events that occur in particle detectors that appear to be anomalous, random and at a certain mass-energy. Statistical methods ought to be able to discern the effects of the beam energy on these events, and therefore we would have a probability that certain anomalous acausal events came from the incident beam. Those events might include tachyons.
See: https://www.quora.com/What-could-prove-tachyons-exist?share=1
* Brout-Englert Higgs mechanism - In the 1970s, physicists realized that there are very close ties between two of the four fundamental forces – the weak force and the electromagnetic force. The two forces can be described within the same theory, which forms the basis of the Standard Model. This “unification” implies that electricity, magnetism, light and some types of radioactivity are all manifestations of a single underlying force known as the electroweak force.
The basic equations of the unified theory correctly describe the electroweak force and its associated force-carrying particles, namely the photon, and the W and Z bosons, except for a major glitch. All of these particles emerge without a mass. While this is true for the photon, we know that the W and Z have mass, nearly 100 times that of a proton. Fortunately, theorists Robert Brout, François Englert and Peter Higgs made a proposal that was to solve this problem. What we now call the Brout-Englert-Higgs mechanism gives a mass to the W and Z when they interact with an invisible field, now called the “Higgs field”, which pervades the universe.
Right after the Big Bang, the Higgs field was zero, but as the universe cooled and the temperature fell below a critical value, the field grew spontaneously so that any particle interacting with it acquired a mass. The more a particle interacts with this field, the heavier it is. Particles like the photon, which do not interact with the Higgs field, are left with no mass at all. Like all fundamental fields, the Higgs field has an associated particle – the Higgs boson. The Higgs boson is the visible manifestation of the Higgs field, rather like a wave at the surface of the sea.
See: https://home.cern/science/physics/origins-brout-englert-higgs-mechanism
Although the Standard Model accurately describes the observable phenomena, it is still incomplete and it does not currently explain tachyons. Perhaps it is only a part of a bigger picture that includes new physics hidden deep in the subatomic world or in the far off dark recesses of the universe.
And, it appears that only Edward Witten and few others, understand his M-Theory, the leading candidate for a unified physical “theory of Everything" (See: https://www.thoughtco.com/m-theory-2699256).
Hartmann352
However intelligent a theory is, we need empirical physics proof is a must. That is the basic characteristic of the scientific method used in modern physics.
All matter around us is made of elementary particles, the building blocks of matter. These particles occur in two basic types called quarks and leptons. Each group consists of six particles, which are related in pairs, or “generations”.
The lightest and most stable particles make up the first generation, whereas the heavier and less-stable particles belong to the second and third generations. All stable matter in the universe is made from particles that belong to the first generation; any heavier particles quickly decay to more stable ones. The six quarks are paired in three generations – the “up quark” and the “down quark” form the first generation, followed by the “charm quark” and “strange quark”, then the “top quark” and “bottom (or beauty) quark”. Quarks also come in three different “colours” and only mix in such ways as to form colourless objects. The six leptons are similarly arranged in three generations – the “electron” and the “electron neutrino”, the “muon” and the “muon neutrino”, and the “tau” and the “tau neutrino”. The electron, the muon and the tau all have an electric charge and a sizeable mass, whereas the neutrinos are electrically neutral and have very little mass.
The neutrino is one of the so-called fundamental particles, which means it isn’t made of any smaller pieces, at least that we know of. Neutrinos are members of the same group as the most famous fundamental particle, the electron (which is powering the device you’re reading this on right now). But while electrons have a negative charge, neutrinos have no charge at all.
Neutrinos are also incredibly small and light. They have some mass, but not much. They are the lightest of all the subatomic particles that have mass. They’re also extremely common—in fact, they’re the most abundant massive particle in the universe. Neutrinos come from all kinds of different sources and are often the product of heavy particles turning into lighter ones, a process called “decay.”
Neutrinos were first predicted in 1930, but they weren’t discovered in experiments until 1956, and scientists thought they were massless until even later. While we keep learning more about neutrinos, with new answers come new mysteries. Physicist Enrico Fermi coined the name “neutrino”, which is Italian for “little neutral one.”
Neutrinos are difficult to study. The only ways they interact is through gravity and the weak force, which is, well, weak. This weak force is important only at very short distances, which means tiny neutrinos can skirt through the atoms of massive objects without interacting. Most neutrinos will pass through Earth without interacting at all. To increase the odds of seeing them, scientists build huge detectors and create intense sources of neutrinos.
There are four fundamental forces at work in the universe: the strong force, the weak force, the electromagnetic force, and the gravitational force. They work over different ranges and have different strengths.
Gravity is the weakest but it has an infinite range. The electromagnetic force also has infinite range but it is many times stronger than gravity. The weak and strong forces are effective only over a very short range and dominate only at the level of subatomic particles. Despite its name, the weak force is much stronger than gravity but it is indeed the weakest of the other three. The strong force, as the name suggests, is the strongest of all four fundamental interactions.
Three of the fundamental forces result from the exchange of force-carrier particles, which belong to a broader group called “bosons”. Particles of matter transfer discrete amounts of energy by exchanging bosons with each other. Each fundamental force has its own corresponding boson – the strong force is carried by the “gluon”, the electromagnetic force is carried by the “photon”, and the “W and Z bosons” are responsible for the weak force. Although not yet found, the “graviton” should be the corresponding force-carrying particle of gravity.
The Standard Model includes the electromagnetic, strong and weak forces and all their carrier particles, and explains well how these forces act on all of the matter particles. However, the most familiar force in our everyday lives, gravity, is not part of the Standard Model, as fitting gravity comfortably into this framework has proved to be a difficult challenge.
The quantum theory used to describe the micro world, and the general theory of relativity used to describe the macro world, are difficult to fit into a single framework. No one has managed to make the two mathematically compatible in the context of the Standard Model. But luckily for particle physics, when it comes to the minuscule scale of particles, the effect of gravity is so weak as to be negligible. Only when matter is in bulk, at the scale of the human body or of the planets for example, does the effect of gravity dominate. So the Standard Model still works well despite its reluctant exclusion of one of the fundamental forces.
Currently, tachyons do not have any current experimental proof. Theoretically tachyons lead to several paradoxes, to the extent that this universe we live in cannot exist if tachyons exist.
The type of universe/universes supporting the existence of tachyons is not currently describable just as every mathematical basis of such universes has not yet been realized. Several non visualizable phenomena including hyper dimensional spaces with mathematical schemes exist and they are often very useful for formulation of visualizable dynamics, too.
Investigate the following for our further edification:
(i) Minkowsky 4 dimensional space-time continuum used to explain special relativistic kinematics and mechanics,
(ii) Riemann space mathematics used by Einstein to obtain the most general (so far) theory of gravity, rectifying Newton’s inverse square law (Newton assumed gravity as instantaneously acting force between any two objects, regardless of their distance of separation, whereas Einstein discovered no interactive force propagates faster than light, due to which there were paradoxes ( Einstein discovered gravity is not a force, but a space-time {nonvisualizable, again} curvature proportional to the mass of the object) with objects gravitationally interacting, while having them separated by such distances that the light takes milli seconds/seconds or minutes/hours as in solar system itself).
Another paper concerning Riemann space and tachyons is 'ON THE RIEMANN HYPOTHESIS AND TACHYONS IN DUAL STRING SCATTERING AMPLITUDES' by Carlos Castro from the Center for Theoretical Studies of Physical Systems Clark Atlanta University, Atlanta, GA, USA
(See: https://vixra.org/pdf/0908.0088v1.pdf )
Castro, in the paper above, explains that "The physical relevance of tachyonic resonances/tachyonic-condensates in bosonic string theory, establishes an important connection between string theory and the Riemann Hypothesis. In addition, one has also a geometrical interpretation of the zeta zeros in the critical line in terms of very special (degenerate) triangular configurations in the upper-part of the complex plane."
(iii) Hilbert space useful in quantum mechanics.
I also suggest that you read Moses Fayngold's book 'Special Relativity and Motion Faster than Light' which covers the ideas about superluminal speeds and special relativity and what happens in theory when objects travel at speeds faster-than-light. Fayngold shows that in all these cases subtle forces of nature conspire to prevent these motions being harnessed to send signals faster than the speed of light.
However, one version of the Standard Model, the string theory with 23 dimensions, supports the existence of tachyons. No other theory includes that possibility, nor is there any evidence.
If you read the Feynman lectures, he does mention that the complete solution of all possible paths for a particle-particle interaction must include particles traveling backwards in time. Reversal of the time direction is not that controversial.
Causality is more than a convenience. Acausal phenomena are extremely hard to either study or contemplate. Like miracles, they just happen. However, the current idea of causality, modified by what happens at the event horizon of a black hole, is pretty far from the simple Aristotelean chain of events. Among other “sacred” ideas, classical causality is already a victim of quantum logic.
All this is preamble to the method to detect a tachyon. They would appear to be acausal. They probably would appear to be traveling backwards in time, which is almost the same as being acausal.
It is assumed that among the tachyons would be at least some with a coefficient of interaction (collision cross-section) that allowed them to be detected in a modern particle chamber, whether they are charged or neutral. I also assume that in such a detector the means of detection involves a collision or other intimate reaction that stops a tachyon. It then converts to a normal particle that registers as an event.
Particle detectors have coincidence detectors that make sure the detected particles come from the beam, and not from incident cosmic rays. Any non-causal event will be filtered out by the coincidence detectors. But those are exactly the kind of events that mark tachyons!
On 4 July 2012, the ATLAS and CMS experiments at CERN's Large Hadron Collider (LHC) announced they had each observed a new particle in the mass region around 126 GeV. This particle is consistent with the Higgs boson but it will take further work to determine whether or not it is the Higgs boson predicted by the Standard Model. The Higgs boson, as proposed within the Standard Model, is the simplest manifestation of the Brout-Englert-Higgs mechanism*. Other types of Higgs bosons are predicted by other theories that go beyond the Standard Model.
We want events that would be filtered out by the coincidence detectors because they do not seem to originate from the beam. Perhaps they really do, but as tachyons, their origin is masked. They just happen. We also want to ignore cosmic ray events.
Tachyon energies are are lower at higher speeds. The closer a tachyon moves to the speed of light, the more mass-energy it has. Given the usual thermal equilibrium of energy in the accelerator’s beam (big assumption here for tachyons) most tachyons will have the same energy as most of that kind of particle. When the tachyon converts to a regular particle, that will be the its contributed mass-energy. Perhaps we can just eliminate events above and below a certain beam energy level.
So we are looking for events that occur in particle detectors that appear to be anomalous, random and at a certain mass-energy. Statistical methods ought to be able to discern the effects of the beam energy on these events, and therefore we would have a probability that certain anomalous acausal events came from the incident beam. Those events might include tachyons.
See: https://www.quora.com/What-could-prove-tachyons-exist?share=1
* Brout-Englert Higgs mechanism - In the 1970s, physicists realized that there are very close ties between two of the four fundamental forces – the weak force and the electromagnetic force. The two forces can be described within the same theory, which forms the basis of the Standard Model. This “unification” implies that electricity, magnetism, light and some types of radioactivity are all manifestations of a single underlying force known as the electroweak force.
The basic equations of the unified theory correctly describe the electroweak force and its associated force-carrying particles, namely the photon, and the W and Z bosons, except for a major glitch. All of these particles emerge without a mass. While this is true for the photon, we know that the W and Z have mass, nearly 100 times that of a proton. Fortunately, theorists Robert Brout, François Englert and Peter Higgs made a proposal that was to solve this problem. What we now call the Brout-Englert-Higgs mechanism gives a mass to the W and Z when they interact with an invisible field, now called the “Higgs field”, which pervades the universe.
Right after the Big Bang, the Higgs field was zero, but as the universe cooled and the temperature fell below a critical value, the field grew spontaneously so that any particle interacting with it acquired a mass. The more a particle interacts with this field, the heavier it is. Particles like the photon, which do not interact with the Higgs field, are left with no mass at all. Like all fundamental fields, the Higgs field has an associated particle – the Higgs boson. The Higgs boson is the visible manifestation of the Higgs field, rather like a wave at the surface of the sea.
See: https://home.cern/science/physics/origins-brout-englert-higgs-mechanism
Although the Standard Model accurately describes the observable phenomena, it is still incomplete and it does not currently explain tachyons. Perhaps it is only a part of a bigger picture that includes new physics hidden deep in the subatomic world or in the far off dark recesses of the universe.
And, it appears that only Edward Witten and few others, understand his M-Theory, the leading candidate for a unified physical “theory of Everything" (See: https://www.thoughtco.com/m-theory-2699256).
Hartmann352
Last edited:
I was rereading this thread and it occurred to me that Max Tegmark addressed the acquisition and emergence of properties as a result of certain patterns and pattern densities.Hey fellas, after 100 yrs of particles, they are still looking for a "mass" particle. What does this tell you? It tells me that our modern science still.....can not discern what "mass" is.
He cited "wetness" as one such emergent properties of a specific pattern of "dry" molecules. H2O is not a wet molecule, but a sufficient quantity of H2O molecules at a certain temperature results in a "wet" liquid (water) The same quantity of H2O molecules at a different temperature may result in a "dry" solid (ice), and yet at a different temperature the same quantity of H2O molecule may result in a "dry" gas (vapor).
Thus H2O has the 3 potential physical expressions dependent on temperature and the resulting pattern arrangement of H2O molecules.

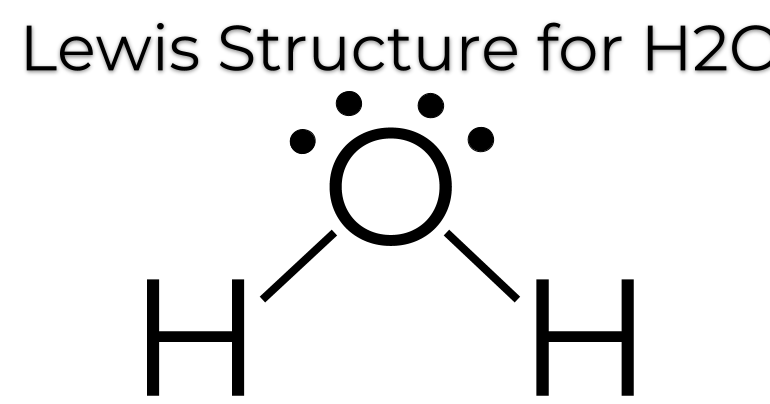
The Lewis Dot Structure for H2O
Learn what the Lewis Dot Structure for H2O is in this post by makethebrainhappy.
It occurred to me that along with the different pattern arrangements the mass of each state also changes, while the weight of the fixed quantity of H2O molecules remains the same.
Am I seeing this correctly?
Remember, write4u, that water is the only known substance which can exist in all three phases: solid, liquid and gas.
Water's special qualities come from the unique shape of the water molecule. Each molecule contains two atoms of hydrogen and one atom of oxygen, arranged such that one side of the molecule (nearest the hydrogens) is positively charged while the other side (nearest the oxygen) is negatively charged. If two water molecules come together, the positive side of one is attracted to the negative side of the other, making the molecules cling together. This simple fact accounts for the high heat capacity, surface tension, cohesion, adhesion, and other characteristics that make water so important to the earth's biosphere.
In general, when considering the states of matter, solids are more dense than liquids and liquids are more dense than gases. Water is a bit of a contrarian in this regard.
When water is in its solid state (ice), the water molecules are packed close together preventing it from changing shape. Ice has a very regular pattern with the molecules rigidly apart from one another connected by the hydrogen bonds that form a crystalline lattice. These crystals have a number of open regions and pockets making ice less dense than liquid water. This is why ice floats on water. Ice forms when the temperature is below freezing (0°Celsius or 32°Fahrenheit).
When ice is warmed above freezing, it melts and becomes liquid water. As a liquid, the attractive forces between molecules weaken and individual molecules can begin to move around each other. Because the molecules can slip and slide around one another, water takes the shape of any container it is in. Despite the "hardness" of ice, the spacing of water molecules per unit volume is actually greater than it is for liquid water. Hence, ice is less dense than liquid water (which is why ice cubes float).
The third state of water is the gaseous state (water vapor). In this state, water molecules move very rapidly and are not bound together. Although we cannot see water in its gaseous state, we can feel it in the air on a hot, humid day. Commonly, water boils at a temperature of 100°C or 212°F, forming water vapor. Many people believe that the visible plume of steam from a boiling kettle is water vapor. However, the steam that you see consists of very small water droplets suspended in the air, while water vapor is the invisible gas that results when water evaporates. We can "see" water vapor through the electromagnetic eyes of infrared-sensing instruments.
Molecules in a liquid don't all have the same energy. The energies of the molecules can vary from a finite minimum, which would mark the transition back to a solid phases, up to an infinite energy (although the probability of this occuring is infinitely small). The average energy of the molecules gives us the temperature of the liquid. Statistical thermodynamics can map out the energy distribution of the water molecules. At a certain energy molecules will have enough energy to evaporate, even if the water temperature is 0 degrees C.
See: https://www.physlink.com/Education/AskExperts/ae282.cfm
A new statistical thermodynamic theory is presented for a model of liquid water, which consists of two components, i.e., tetrahedrally-coordinated pentamers and non-hydrogen-bonded monomers.
In the model the two components are assumed to be immersed in a uniform background potential which results from electrostatic, induction, and dispersion forces between water molecules.
A partition function is given without assuming any specified lattice. A translational partition function is written into a simple and explicit expression which is derived from the Lebowitz solution of the Percus-Yevick equation for hard sphere mixtures. The mole fraction of each component and the density are determined by solving two equations, i.e., the condition of free energy minimization and the equation of state derived from the partition function, simultaneously. Various thermodynamic quantities are calculated and the values determined are compared with those observed. Some discussions are carried out, together with the criticism of the earlier theories.
See: https://www.journal.csj.jp/doi/10.1246/bcsj.50.65
It is actually possible to create a stable and dry form of water. It’s hardly a new invention, having been developed in 1968, but interest in dry water is suddenly surging. Researchers are only now discovering some of the potential applications for it, such as using it to store carbon dioxide or methane, and in the fuel cells that may power automobiles.
A more accurate name for dry water is powdered water. It is a white powder, similar in appearance to sugar, that is easily pourable. The makeup of powdered water is about 95 percent water. The remainder is silica, an abundant material found mostly on beaches. Each grain of the dry water consists of a drop of water surrounded by particles of silica. These silica particles prevent the suspended water droplets from coalescing back into a liquid because they are hydrophobic (non-polar).
Dry water’s most important characteristic is its ability to absorb gases. In fact, a recent experiment demonstrated that the dry water powder is capable of absorbing three times as much carbon dioxide as the same amount of liquid water and silica. Scientists find this ability to absorb gases very exciting, as it could be used as a greenhouse gas sequestration agent. Potentially, engineers could develop a way to trap carbon dioxide and other gases quickly and cheaply at the source. The gas combines with particles of dry water to form a hydrate, which keeps the gas from ever entering the atmosphere.
Another possible use of dry water powder is as a storage and transportation mechanism for volatile gases like methane and propane. Since the gases absorbed by dry water are not permanently bound to the water particles, it would be a relatively simple matter to remove the gases when they are needed. This could potentially prove very useful in automobiles running on natural gas or fuel cells. One major problem facing these vehicles is the difficulty of safely storing volatile gases like hydrogen and methane; if the gases can instead be stored in a powder, the need for expensive and bulky gas-storage tanks would be eliminated.
Some scientists also suggest that powdered water might be used to absorb seabed deposits of natural gas that are too difficult to retrieve by standard methods. Interestingly, something like dry water already exists at these extreme depths. At the sea floor gas hydrates sometimes form; this is a type of frozen methane often called “ice that burns.”
Professor Andrew Cooper has reported that his research team has developed a method for creating dry water emulsions. An emulsion is a mixture of liquids that do not dissolve in one another, like milk. The team demonstrated a technique to turn an emulsion into a dry powder, much like dry water. This could help industry transport and store dangerous liquids with an added degree of safety, as the powdered form would be less reactive.
Cooper’s team also demonstrated a method for using dry water in reactions between hydrogen and maleic acid. This reaction creates succinic acid, which is a material used to manufacture drugs, various foods, and other products. The reaction normally requires extensive stirring to occur, but scientists have shown that creating a dry water hydrate with maleic acid speeds up the reaction. This method also eliminates the need for stirring, which would result in a substantial energy savings.
See: https://www.brighthubengineering.co...gy/86654-and-now-science-brings-us-dry-water/
Water cycles endlessly throughout the atmosphere, oceans, land, and life of planet earth, taking each physical state at one time or another while providing a marvelous basis for all life. Additionally, dry water is found to have numerous scientific and manufacturing uses.
Hartmann352
Water's special qualities come from the unique shape of the water molecule. Each molecule contains two atoms of hydrogen and one atom of oxygen, arranged such that one side of the molecule (nearest the hydrogens) is positively charged while the other side (nearest the oxygen) is negatively charged. If two water molecules come together, the positive side of one is attracted to the negative side of the other, making the molecules cling together. This simple fact accounts for the high heat capacity, surface tension, cohesion, adhesion, and other characteristics that make water so important to the earth's biosphere.
In general, when considering the states of matter, solids are more dense than liquids and liquids are more dense than gases. Water is a bit of a contrarian in this regard.
When water is in its solid state (ice), the water molecules are packed close together preventing it from changing shape. Ice has a very regular pattern with the molecules rigidly apart from one another connected by the hydrogen bonds that form a crystalline lattice. These crystals have a number of open regions and pockets making ice less dense than liquid water. This is why ice floats on water. Ice forms when the temperature is below freezing (0°Celsius or 32°Fahrenheit).
When ice is warmed above freezing, it melts and becomes liquid water. As a liquid, the attractive forces between molecules weaken and individual molecules can begin to move around each other. Because the molecules can slip and slide around one another, water takes the shape of any container it is in. Despite the "hardness" of ice, the spacing of water molecules per unit volume is actually greater than it is for liquid water. Hence, ice is less dense than liquid water (which is why ice cubes float).
The third state of water is the gaseous state (water vapor). In this state, water molecules move very rapidly and are not bound together. Although we cannot see water in its gaseous state, we can feel it in the air on a hot, humid day. Commonly, water boils at a temperature of 100°C or 212°F, forming water vapor. Many people believe that the visible plume of steam from a boiling kettle is water vapor. However, the steam that you see consists of very small water droplets suspended in the air, while water vapor is the invisible gas that results when water evaporates. We can "see" water vapor through the electromagnetic eyes of infrared-sensing instruments.
Molecules in a liquid don't all have the same energy. The energies of the molecules can vary from a finite minimum, which would mark the transition back to a solid phases, up to an infinite energy (although the probability of this occuring is infinitely small). The average energy of the molecules gives us the temperature of the liquid. Statistical thermodynamics can map out the energy distribution of the water molecules. At a certain energy molecules will have enough energy to evaporate, even if the water temperature is 0 degrees C.
See: https://www.physlink.com/Education/AskExperts/ae282.cfm
A new statistical thermodynamic theory is presented for a model of liquid water, which consists of two components, i.e., tetrahedrally-coordinated pentamers and non-hydrogen-bonded monomers.
In the model the two components are assumed to be immersed in a uniform background potential which results from electrostatic, induction, and dispersion forces between water molecules.
A partition function is given without assuming any specified lattice. A translational partition function is written into a simple and explicit expression which is derived from the Lebowitz solution of the Percus-Yevick equation for hard sphere mixtures. The mole fraction of each component and the density are determined by solving two equations, i.e., the condition of free energy minimization and the equation of state derived from the partition function, simultaneously. Various thermodynamic quantities are calculated and the values determined are compared with those observed. Some discussions are carried out, together with the criticism of the earlier theories.
See: https://www.journal.csj.jp/doi/10.1246/bcsj.50.65
It is actually possible to create a stable and dry form of water. It’s hardly a new invention, having been developed in 1968, but interest in dry water is suddenly surging. Researchers are only now discovering some of the potential applications for it, such as using it to store carbon dioxide or methane, and in the fuel cells that may power automobiles.
A more accurate name for dry water is powdered water. It is a white powder, similar in appearance to sugar, that is easily pourable. The makeup of powdered water is about 95 percent water. The remainder is silica, an abundant material found mostly on beaches. Each grain of the dry water consists of a drop of water surrounded by particles of silica. These silica particles prevent the suspended water droplets from coalescing back into a liquid because they are hydrophobic (non-polar).
Dry water’s most important characteristic is its ability to absorb gases. In fact, a recent experiment demonstrated that the dry water powder is capable of absorbing three times as much carbon dioxide as the same amount of liquid water and silica. Scientists find this ability to absorb gases very exciting, as it could be used as a greenhouse gas sequestration agent. Potentially, engineers could develop a way to trap carbon dioxide and other gases quickly and cheaply at the source. The gas combines with particles of dry water to form a hydrate, which keeps the gas from ever entering the atmosphere.
Another possible use of dry water powder is as a storage and transportation mechanism for volatile gases like methane and propane. Since the gases absorbed by dry water are not permanently bound to the water particles, it would be a relatively simple matter to remove the gases when they are needed. This could potentially prove very useful in automobiles running on natural gas or fuel cells. One major problem facing these vehicles is the difficulty of safely storing volatile gases like hydrogen and methane; if the gases can instead be stored in a powder, the need for expensive and bulky gas-storage tanks would be eliminated.
Some scientists also suggest that powdered water might be used to absorb seabed deposits of natural gas that are too difficult to retrieve by standard methods. Interestingly, something like dry water already exists at these extreme depths. At the sea floor gas hydrates sometimes form; this is a type of frozen methane often called “ice that burns.”
Professor Andrew Cooper has reported that his research team has developed a method for creating dry water emulsions. An emulsion is a mixture of liquids that do not dissolve in one another, like milk. The team demonstrated a technique to turn an emulsion into a dry powder, much like dry water. This could help industry transport and store dangerous liquids with an added degree of safety, as the powdered form would be less reactive.
Cooper’s team also demonstrated a method for using dry water in reactions between hydrogen and maleic acid. This reaction creates succinic acid, which is a material used to manufacture drugs, various foods, and other products. The reaction normally requires extensive stirring to occur, but scientists have shown that creating a dry water hydrate with maleic acid speeds up the reaction. This method also eliminates the need for stirring, which would result in a substantial energy savings.
See: https://www.brighthubengineering.co...gy/86654-and-now-science-brings-us-dry-water/
Water cycles endlessly throughout the atmosphere, oceans, land, and life of planet earth, taking each physical state at one time or another while providing a marvelous basis for all life. Additionally, dry water is found to have numerous scientific and manufacturing uses.
Hartmann352
"I was rereading this thread and it occurred to me that Max Tegmark addressed the acquisition and emergence of properties as a result of certain patterns and pattern densities."
He is trying to rationalize and narrate the source of matter properties, via, about the only thing that we can measure when dealing with small bits of matter. Which is an induced or reflected EM radio pattern. Science has tried for many decades to make sense of these patterns. And their spectrums.
But, the changing patterns are a direct result of a change in the dimensions, density and motion in the fundamental dipole structure. The structure of the dipoles change length, size, shape, density and spin rate with temperature. They are just like quantum steps and stable at only certain dimensions. There is a range of these dimensions for each state.
So the patterns are a result, not a cause. The cause is the electrical and physical tuning of the dipoles. And only certain tunes can be played.
He is trying to rationalize and narrate the source of matter properties, via, about the only thing that we can measure when dealing with small bits of matter. Which is an induced or reflected EM radio pattern. Science has tried for many decades to make sense of these patterns. And their spectrums.
But, the changing patterns are a direct result of a change in the dimensions, density and motion in the fundamental dipole structure. The structure of the dipoles change length, size, shape, density and spin rate with temperature. They are just like quantum steps and stable at only certain dimensions. There is a range of these dimensions for each state.
So the patterns are a result, not a cause. The cause is the electrical and physical tuning of the dipoles. And only certain tunes can be played.
So the patterns are a result, not a cause. The cause is the electrical and physical tuning of the dipoles. And only certain tunes can be played.
I understand but it is only the pattern that is measurable and acquires properties over and above the sum and properties of the constituent parts?
Is this not explained by Chaos Theory ?
Description
Chaos theory is an interdisciplinary scientific theory and branch of mathematics focused on underlying patterns and deterministic laws, of dynamical systems, that are highly sensitive to initial conditions, that were once thought to have completely random states of disorder and irregularities. Wikipedia
I am always intrigued by the beautiful patterns that emerge from dynamical systems.
A particle is a pure tone, which is modulated with a wobble. A dipole is two part harmony. Atoms and molecules are a chorus. A spectrum. These tunes, harmonies and spectrums have been constant since the beginning. The exact same songs. Same tunes. One permanent jukebox with a fixed library.
This fact alone implies, that randomness, probability and chaos does not exist with nature.
This fact alone implies, that randomness, probability and chaos does not exist with nature.
Music of the spheres (strings) ...i.e. "relational values".A particle is a pure tone, which is modulated with a wobble. A dipole is two part harmony. Atoms and molecules are a chorus. A spectrum. These tunes, harmonies and spectrums have been constant since the beginning. The exact same songs. Same tunes. One permanent jukebox with a fixed library.
This fact alone implies, that randomness, probability and chaos does not exist with nature.
Does that not suggest a universal generic mathematical potential, what David Bohm called the "enfolded order"?
And explains why human codified symbolic mathematics work so well?
Last edited:
Not spheres........compound rings. From a compound radius. A ring with a helical circumference. A small helical circumference modulates(wobbles) the rotation of the ring. One rotation of the ring can posses many rotations of the helix of the circumference. Many rotations within one rotation. The balance of the fields of this structure is called inertia.....mass. Rest Mass. These balanced fields will resist acceleration.
The ratio of these two rotations is discreet, filtered and fixed. Quantum steps.
As soon as science discovered these fixed steps, they should have reasoned that randomness and probability do not exist with matter. DUH. I have never understood that.
So there is a fundamental order. It's a ratio. A ratio of physical field balance. If the ratio was a math entity, we could make that ratio at will. BUT that ratio, that relationship, is NOT mathematical, it's physical. It's selective and discreet......NOT mathematical.
Math can only inventory mass and energy, math can not explain or narrate mass and energy. Math is just a tool. Besides, energy and mass are properties, not entities. The only physical entity in this universe is charge, and the EM field from it. That's all physicality is. That's all that's needed for all this to exist.
Math is not needed to explain or narrate physicality. This narrative only explains mass and matter, and the products of it, light and gravity. Neither this narrative or any other narrative, observation, or measurement can answer the questions that science and philosophers have. Many questions will never be answered by our tools or intellect. But, I do believe that the present physicality can be explained and understood. Math has infinite solutions, physicality has one.
The ratio of these two rotations is discreet, filtered and fixed. Quantum steps.
As soon as science discovered these fixed steps, they should have reasoned that randomness and probability do not exist with matter. DUH. I have never understood that.
So there is a fundamental order. It's a ratio. A ratio of physical field balance. If the ratio was a math entity, we could make that ratio at will. BUT that ratio, that relationship, is NOT mathematical, it's physical. It's selective and discreet......NOT mathematical.
Math can only inventory mass and energy, math can not explain or narrate mass and energy. Math is just a tool. Besides, energy and mass are properties, not entities. The only physical entity in this universe is charge, and the EM field from it. That's all physicality is. That's all that's needed for all this to exist.
Math is not needed to explain or narrate physicality. This narrative only explains mass and matter, and the products of it, light and gravity. Neither this narrative or any other narrative, observation, or measurement can answer the questions that science and philosophers have. Many questions will never be answered by our tools or intellect. But, I do believe that the present physicality can be explained and understood. Math has infinite solutions, physicality has one.
At what point is something no longer physical? One can say that a ratio or quantity is a physical object, but would that not be a semantic trick?So there is a fundamental order. It's a ratio. A ratio of physical field balance. If the ratio was a math entity, we could make that ratio at will. BUT that ratio, that relationship, is NOT mathematical, it's physical. It's selective and discreet......NOT mathematical.
Ratio, noun
Oxford Dictionarythe quantitative relation between two amounts showing the number of times one value contains or is contained within the other.
IOW, "ratio" is a mathematical differential equation between 2 relational values a mathematical condition.
Human symbolic mathematics is just a tool to explain everything we know about physics.Math can only inventory mass and energy, math can not explain or narrate mass and energy. Math is just a tool.
I am talking about a generic mathematical function that allows for the orderly interaction between "relational values", that are inherent potentials of both qualitative and quantitative values and ratios between values.
As far as I understand Bohmian mechanics, the "implicate or potential order" is the generic mathematical essence of all physical objects and the "guiding principle" of the way the implicate becomes expressed as the "explicate or physical order".
And "charge" is a value, no?Besides, energy and mass are properties, not entities. The only physical entity in this universe is charge, and the EM field from it.
Can't very well work with the words "charge" without identifying "how much".
I agree with that but how does this chaotic EM field operate?That's all physicality is. That's all that's needed for all this to exist.
Chaos theory
Chaos theory is an interdisciplinary scientific theory and branch of mathematics focused on underlying patterns and deterministic laws, of dynamical systems, that are highly sensitive to initial conditions, that were once thought to have completely random states of disorder and irregularities. Wikipedia
All physical descriptions in science are symbolized by mathematically codified descriptions of regular and recurring atomic and molecular patterns and patterns are mathematical objects.
It is the mathematical patterns that acquire the physical properties we observe.
I know this perspective may seem simplistic, but it should not be complicated. As far as I know, there is no 'irreducibly complex physical thing".
A deterministically operating universe has to be mathematical in essence. The term physics means nothing without "differential equations".
(and I am not talking about human maths)
I believe an interesting treatise supporting my perspective, may be found :

Mathematics & Reality
Raymond Tallis on maths’ unreasonable effectiveness.
The belief that mathematics is the surest path to the truth about the universe because the latter is at bottom mathematical has been very influential in Western thought. It goes back to Pythagoras’s assertion that “All is number,” or, as Aristotle paraphrased it, “The principles of mathematics are the principles of all things.” It is the rationale behind Plato’s insistence that no one should enter his Academy without knowledge of geometry.
You just cited several mathematical properties in relation to the fundamental dynamical structure of spacetime.Hayseed said:
A small helical circumference modulates(wobbles) the rotation of the ring. One rotation of the ring can possess many rotations of the helix of the circumference.
And in reference to Pythagoras’s discovery of the mathematical ratios underlying pitch, such that doubling the length of a string on a musical instrument produces a note an octave lower, has resonated long and loud through human consciousness. Galileo’s assertion that “The book of nature is written in the language of mathematics” has been a guiding principle of science since the scientific revolution to which he contributed so much.
The idea of the universe as a gigantic computer, and the belief that everything (including conscious experience) is information that is either itself digital or can be digitized without loss, is but a recent manifestation of Pythagoreanism.
Mathematics & Reality | Issue 102 | Philosophy Now
Raymond Tallis on maths’ unreasonable effectiveness.
These geniuses were all wrong???
What is the valid objection to the concept of a mathematical essence to universal geometry and dynamics?
Last edited:
Again, this is not working out very well. You insist on using math concepts for physicality. You are using math terms as a reference for explanation. All of my terms are physical terms, not mathematical. You had to be taught this, and evidently it gives you comfort.
For instance. Ratio. You want to find a common divisor. A number relationship between the two quantities. Some think it has meaning. What about a ratio in which the common divisor, is constantly changing?
But to me, a ratio is a comparison of or a balance of properties. A physical ratio. Only certain ratios can exist in physicality. Physicality is restricted and limited due to handedness. Handedness is the cause of asymmetrical matter, that is, the energy, mass and size difference between electrons and protons. But without that handedness, there would be no matter at all. If the charges were the same energy and size, all the charges could physically touch, and would disintegrate each other into EM radio. No particles and no matter would exist. All matter would convert into EM radio. This solves the so called mystery of anti matter. It's just regular matter in an inverted handed state.
Our two completely different references of basic understanding, is probably why we don't understand one another, and just keep repeating ourselves.
I can not help you with a math narrative. It has no force, power or authority. It only exist between the ears.
Physicality is so, so, so much more than math. It's as close to perfection that science can get. Science has no idea of this. It's spectacular and elegant. The elegance alone is worth the time to study it. And it relates all of physical science to one fundamental.
If we went out in space and took one point, or one small area of space, the EM we detected would appear to be chaotic. It's called static. Some call it quantum foam. There would be multiple EM emissions, with different amplitudes, with different durations, and with different directions. Chaos. But only because of our small observation area. If we use the whole universe as the observation area, freeze time, we could track and see where each and every EM came from. And the apparent chaos disappears and the static will depend on our position and time in space, relative to all the times and distances of all the emissions. It's not at all random or chaotic....or probability. With enough data.....the so called chaos is predictable.
The same applies to a particle flux. There is no chaos. Just missing data. And an improper narrative.
My statements only apply to non living matter. Nature.
I do agree that science has given math authority over it. And just about all science now has a very strong math context. And it has really stymied fundamental understanding. One hundred years and we can't draw an electron and still have no narrative for mass. With math leading all the way.
But I digress.
For instance. Ratio. You want to find a common divisor. A number relationship between the two quantities. Some think it has meaning. What about a ratio in which the common divisor, is constantly changing?
But to me, a ratio is a comparison of or a balance of properties. A physical ratio. Only certain ratios can exist in physicality. Physicality is restricted and limited due to handedness. Handedness is the cause of asymmetrical matter, that is, the energy, mass and size difference between electrons and protons. But without that handedness, there would be no matter at all. If the charges were the same energy and size, all the charges could physically touch, and would disintegrate each other into EM radio. No particles and no matter would exist. All matter would convert into EM radio. This solves the so called mystery of anti matter. It's just regular matter in an inverted handed state.
Our two completely different references of basic understanding, is probably why we don't understand one another, and just keep repeating ourselves.
I can not help you with a math narrative. It has no force, power or authority. It only exist between the ears.
Physicality is so, so, so much more than math. It's as close to perfection that science can get. Science has no idea of this. It's spectacular and elegant. The elegance alone is worth the time to study it. And it relates all of physical science to one fundamental.
If we went out in space and took one point, or one small area of space, the EM we detected would appear to be chaotic. It's called static. Some call it quantum foam. There would be multiple EM emissions, with different amplitudes, with different durations, and with different directions. Chaos. But only because of our small observation area. If we use the whole universe as the observation area, freeze time, we could track and see where each and every EM came from. And the apparent chaos disappears and the static will depend on our position and time in space, relative to all the times and distances of all the emissions. It's not at all random or chaotic....or probability. With enough data.....the so called chaos is predictable.
The same applies to a particle flux. There is no chaos. Just missing data. And an improper narrative.
My statements only apply to non living matter. Nature.
I do agree that science has given math authority over it. And just about all science now has a very strong math context. And it has really stymied fundamental understanding. One hundred years and we can't draw an electron and still have no narrative for mass. With math leading all the way.
But I digress.
You deny that it is even possible that the universe has a mathematical aspect to it.But, the changing patterns are a direct result of a change in the dimensions, density and motion in the fundamental dipole structure. The structure of the dipoles change length, size, shape, density and spin rate with temperature. They are just like quantum steps and stable at only certain dimensions. There is a range of these dimensions for each state.
Yet in your countering argument, you are freely using mathematical terms as if they exclusively belonged to the realm of physics.
Tegmark observed that most physicists assign some mathematical properties to the universe. He just extends this notion that universe has only mathematical properties, which seems entirely reasonable as it allows us to quantify and qualify natural phenomena and acquire greater understanding of the way things work.
No, I don't want to find anything.For instance. Ratio. You want to find a common divisor. A number relationship between the two quantities. Some think it has meaning. What about a ratio in which the common divisor, is constantly changing?
"Ratio is a mathematical term by definition".
Whether ratios are fixed or variable, they do not change definition.
Until recently we had no access to pico scale events.One hundred years and we can't draw an electron and still have no narrative for mass. With math leading all the way.
Pretty hard to describe an object without observation.
And therein lies the crux. We cannot physically describe an electron but we can measure its mathematical properties (potentials).
The following illustrates the necessity for "relational values" and "mathematically ordered" processes.

Properties of the electron
Physicists currently think that the electron is a fundamental particle. As with any particle at this scale, it can only be defined by its properties. Some of these properties can be measured in the school laboratory. There is enormous benefit to intermediate and advanced students of seeing some...
I am absolutely sure Tegmark does not mean that human maths are sufficient to describe all universal mathematics. Human maths is a codified symbolic language, gleaned from observed natural relational behaviors and it is certain that we have not observed everything. But we have been able to mathematically predict events and AFAIK, that counts as proof. Is that not how Einstein predicted gravitational lensing?
But, to my knowledge (I admit my limitations), there is no physical functional descriptions of any physical behaviors from quantum to gross expression, without the use of the logical language of mathematics.
We can't draw a picture of a Higgs boson, but via applied mathematical physics we can make it physically manifest for an instant.
Question: If symmetry is a mathematical expression why do we use the term symmetry breaking in fundamental physics?
Is this from observation or pure invention?
Why is symmetry a great example of mathematical concept?
Why Teach Symmetry?By looking at symmetry in a broader context, students can see the interconnectedness of mathematics with other branches of knowledge. For these reasons, many mathematicians today feel that the mathematical study of symmetry is worthwhile for general education students to explore
Symmetry is found everywhere in nature and is also one of the most prevalent themes in art, architecture, and design — in cultures all over the world and throughout human history.
Symmetry is certainly one of the most powerful and pervasive concepts in mathematics.
In the Elements, Euclid exploited symmetry from the very first proposition to make his proofs clear and straightforward. Recognizing the symmetry that exists among the roots of an equation, Galois was able to solve a centuries-old problem.
The tool that he developed to understand symmetry, namely group theory, has been used by mathematicians ever since to define, study, and even create symmetry.
Symmetry — A Link Between Mathematics and Life | Maharishi International University | Accredited & Nonprofit
By Cathy Gorini Introduction In mathematics, certain basic concepts, such as symmetry and infinity, are so pervasive and adaptable that they can become elusive to the student. Understanding these concepts and the tools for studying them is often a long process that extends over many years in a...
Last edited:
Tegmark observes: "Most scientists recognize some mathematical properties to the universe. I recognize only mathematical properties."
This concept was originally developed by Eugene Wigner in his paper:
"The Unreasonable Effectiveness of Mathematics in the Natural Sciences" by Eugene Wigner.
See the initial elements of Wigner's paper below. Feel free to read it to conclusion:
The first point is that mathematical concepts turn up in entirely unexpected con- nections. Moreover, they often permit an unexpectedly close and accurate description of the phenomena in these connections. Secondly, just because of this circumstance, and because we do not understand the reasons of their usefulness, we cannot know whether a theory formulated in terms of mathematical concepts is uniquely appropriate. We are in a position similar to that of a man who was provided with a bunch of keys and who, having to open several doors in succession, always hit on the right key on the first or second trial. He became skeptical concerning the uniqueness of the coordination between keys and doors.
Most of what will be said on these questions will not be new; it has probably occurred to most scientists in one form or another. My principal aim is to illuminate it from several sides. The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.
Second, it is just this uncanny usefulness of mathematical concepts that raises the question of the uniqueness of our physical theories. In order to establish the first point, that mathematics plays an unreasonably important role in physics, it will be useful to say a few words on the question, “What is mathematics?”, then, “What is physics?”, then, how mathematics enters physical theories, and last, why the success of mathematics in its role in physics appears so baffling. Much less will be said on the second point: the uniqueness of the theories of physics. A proper answer to this question would require elaborate experimental and theoretical work which has not been undertaken to date.
I would say that mathematics is the science of skillful operations with concepts and rules invented just for this purpose. The principal emphasis is on the invention of concepts. Mathematics would soon run out of interesting theorems if these had to be formulated in terms of the concepts which already appear in the axioms. Furthermore, whereas it is unquestionably true that the concepts of elementary mathematics and particularly
elementary geometry were formulated to describe entities which are directly suggested by the actual world, the same does not seem to be true of the more advanced concepts, in particular the concepts which play such an important role in physics. Thus, the rules for operations with pairs of numbers are obviously designed to give the same results as the operations with fractions which we first learned without reference to “pairs of numbers.” The rules for the operations with sequences, that is, with irrational numbers, still belong to the category of rules which were determined so as to reproduce rules for the operations with quantities which were already known to us. Most more advanced mathematical concepts, such as complex numbers, algebras, linear operators, Borel sets, and this list could be continued almost indefinitely, were so devised that they are apt subjects on which the mathematician can demonstrate his ingenuity and sense of formal beauty. In fact, the definition of these concepts, with a realization that interesting and ingenious considerations could be applied to them, is the first demonstration of the ingeniousness of the mathematician who defines them. The depth of thought which goes into the formulation of the mathematical concepts is later justified by the skill with which these
concepts are used. The great mathematician fully, almost ruthlessly, exploits the domain of
permissible reasoning and skirts the impermissible. That his recklessness does not lead him into a morass of contradictions is a miracle in itself: certainly it is hard to believe that our reasoning power was brought, by Darwin’s process of natural selection, to the perfection which it seems to possess. However, this is not our present subject. The principal point which will have to be recalled later is that the mathematician could formulate only a handful of interesting theorems without defining concepts beyond those contained in the axioms and that the concepts outside those contained in the axioms are defined with a view of permitting ingenious logical operations which appeal to our aesthetic sense both as operations and also in their results of great generality.
Polanyi, in his Personal Knowledge (Chicago: University of Chicago Press, 1958), says: “All these difficulties are but consequences of our refusal to see that mathematics cannot be defined without acknowledging its most obvious feature: namely, that it is interesting” (p 188).
Certainly, nothing in our experience suggests the introduction of these quantities. Indeed, if a mathematician is asked to justify his interest in complex numbers, he will point, with some indignation, to the many beautiful theorems in the theory of equations, of power series, and of analytic functions in general, which owe their origin to the introduction of complex numbers. The mathematician is not willing to give up his interest in these most beautiful accomplishments of his genius.
The physicist is interested in discovering the laws of inanimate nature. In order to understand this statement, it is necessary to analyze the concept, “law of nature.” The world around us is of baffling complexity and the most obvious fact about it is that we cannot predict the future. Although the joke attributes only to the optimist the view that the future is uncertain, the optimist is right in this case: the future is unpredictable. It is, as Schrodinger has remarked, a miracle that in spite of the baffling complexity of the world, certain regularities in the events could be discovered. One such regularity, discovered by Galileo, is that two rocks, dropped at the same time from the same height, reach the ground at the same time. The laws of nature are concerned with such regularities. Galileo’s regularity is a prototype of a large class of regularities. It is a surprising regularity for three reasons.
The first reason that it is surprising is that it is true not only in Pisa, and in Galileo’s time,
it is true everywhere on the Earth, was always true, and will always be true. This property
of the regularity is a recognized invariance property and, as I had occasion to point out some time ago, without invariance principles similar to those implied in the preceding generalization of Galileo’s observation, physics would not be possible. The second surprising feature is that the regularity which we are discussing is independent of so many conditions which could have an effect on it. It is valid no matter whether it rains or not, whether the experiment is carried out in a room or from the Leaning Tower, no matter whether the person who drops the rocks is a man or a woman. It is valid even if the two rocks are dropped, simultaneously and from the same height, by two different people. There are, obviously, innumerable other conditions which are all immaterial from the point of view of the validity of Galileo’s regularity. The irrelevancy of so many circumstances which could play a role in the phenomenon observed has also been called an invariance. However, this invariance is of a different character from the preceding one since it cannot be formulated as a general principle. The exploration of the conditions which do, and which do not, influence a phenomenon is part of the early experimental exploration of a field. It is the skill and ingenuity of the experimenter which show him phenomena which depend on a relatively narrow set of relatively easily realizable and reproducible conditions. In the present case, Galileo’s restriction of his observations to relatively heavy bodies was the most important step in this regard. Again, it is true that if there were no phenomena which are independent of all but a manageably small set of conditions, physics would be impossible.
The preceding two points, though highly significant from the point of view of the philosopher, are not the ones which surprised Galileo most, nor do they contain a specific law of nature. The law of nature is contained in the statement that the length of time which it takes for a heavy object to fall from a given height is independent of the size, material, and shape of the body which drops. In the framework of Newton’s second “law,” this amounts to the statement that the gravitational force which acts on the falling body is proportional to its mass but independent of the size, material, and shape of the body which falls.
In the present case, Galileo’s restriction of his observations to relatively heavy bodies was the most important step in this regard. Again, it is true that if there were no phenomena which are independent of all but a manageably small set of conditions, physics would be impossible.
The present writer had occasion some time ago, to call attention to the succession of layers of “laws of nature,” each layer containing more general and more encompassing laws than the previous one and its discovery constituting a deeper penetration into the structure of the universe than the layers recognized before. However, the point which is most significant in the present context is that all these laws of nature contain, in even their remotest consequences, only a small part of our knowledge of the inanimate world. All the laws of nature are conditional statements which permit a prediction of some future events on the basis of the knowledge of the present, except that some aspects of the present state of the world, in practice the overwhelming majority of the determinants of the present state of the world, are irrelevant from the point of view of the prediction.
As regards the present state of the world, such as the existence of the earth on which we live and on which Galileo’s experiments were performed, the existence of the sun and of all our surroundings, the laws of nature are entirely silent. It is in consonance with this, first, that the laws of nature can be used to predict future events only under exceptional circumstances when all the relevant determinants of the present state of the world are known. It is also in consonance with this that the construction of machines, the functioning of which he can foresee, constitutes the most spectacular accomplishment of the physicist. In these machines, the physicist creates a situation in which all the relevant coordinates are known so that the behavior of the machine can be predicted. Radars and nuclear reactors are examples of such machines.
The principal purpose of the preceding discussion is to point out that the laws of nature are all conditional statements and they relate only to a very small part of our knowledge of the world. Thus, classical mechanics, which is the best known prototype of a physical theory, gives the second derivatives of the positional coordinates of all bodies, on the basis of the knowledge of the positions, etc., of these bodies. It gives no information on the existence, the present positions, or velocities of these bodies. It should be mentioned, for the sake of accuracy, that we discovered about thirty years ago that even the conditional statements cannot be entirely precise: that the conditional statements are probability laws which enable us only to place intelligent bets on future properties of the inanimate world, based on the knowledge of the present state. They do not allow us to make categorical statements, not even categorical statements conditional on the present state of the world. The probabilistic nature of the “laws of nature” manifests itself in the case of machines also, and can be verified, at least in the case of nuclear reactors, if one runs them at very low power. However, the additional limitation of the scope of the laws of nature which follows from their probabilistic nature will play no role in the rest of the discussion.
Having refreshed our minds as to the essence of mathematics and physics, we should be in a better position to review the role of mathematics in physical theories. Naturally, we do use mathematics in everyday physics to evaluate the results of the laws of nature, to apply the conditional statements to the particular conditions which happen to prevail or happen to interest us. In order that this be possible, the laws of nature must already be formulated in mathematical language. However, the role of evaluating the consequences of already established theories is not the most important role of mathematics in physics.
Mathematics does play, however, also a more sovereign role in physics. This was already implied in the statement, made when discussing the role of applied mathematics, that the laws of nature must have been formulated in the language of mathematics to be an object for the use of applied mathematics. The statement that the laws of nature are written in the language of mathematics was properly made three hundred years ago;9 it is now more true than ever before. In order to show the importance which mathematical concepts possess in the formulation of the laws of physics, let us recall, as an example, the axioms of quantum mechanics as formulated, explicitly, by the great physicist, Dirac. There are two basic concepts in quantum mechanics: states and observables. The states are vectors in Hilbert space, the observables self-adjoint operators on these vectors. The possible values of the observations are the characteristic values of the operators but we had better stop here lest we engage in a listing of the mathematical concepts developed in the theory of linear operators.
See: http://www.hep.upenn.edu/~johnda/Papers/wignerUnreasonableEffectiveness.pdf
Eugene Wigner, in full Eugene Paul Wigner, Hungarian Jenó Pál Wigner, (born November 17, 1902, Budapest, Hungary, Austria-Hungary—died January 1, 1995, Princeton, New Jersey, U.S.), Hungarian-born American physicist, joint winner, with J. Hans D. Jensen of West Germany and Maria Goeppert Mayer of the United States, of the Nobel Prize for Physics in 1963.
He received the prize for his many contributions to nuclear physics, which include his formulation of the law of conservation of parity.
Wigner studied chemical engineering and received a Ph.D. from the Institute of Technology in Berlin in 1925. After serving as a lecturer there and at the University of Göttingen, he emigrated to the United States.
Apart from two years (1936–38) as professor of physics at the University of Wisconsin, he spent his academic life at Princeton University, serving as a professor of mathematical physics from 1938 until his retirement in 1971. He became a naturalized U.S. citizen in 1937.
See: https://www.britannica.com/biography/Eugene-Wigner
Wigner is telling us , first, that it is not at all natural that “laws of nature” exist, much less that man is able to discover them. He is also explains that mathematics, or, rather, applied mathematics, is not so much the master of the situation in this function: it is merely serving as a tool. A tool to explain the natural processes unfolding in the universe.
Hartmann352
This concept was originally developed by Eugene Wigner in his paper:
"The Unreasonable Effectiveness of Mathematics in the Natural Sciences" by Eugene Wigner.
See the initial elements of Wigner's paper below. Feel free to read it to conclusion:
The first point is that mathematical concepts turn up in entirely unexpected con- nections. Moreover, they often permit an unexpectedly close and accurate description of the phenomena in these connections. Secondly, just because of this circumstance, and because we do not understand the reasons of their usefulness, we cannot know whether a theory formulated in terms of mathematical concepts is uniquely appropriate. We are in a position similar to that of a man who was provided with a bunch of keys and who, having to open several doors in succession, always hit on the right key on the first or second trial. He became skeptical concerning the uniqueness of the coordination between keys and doors.
Most of what will be said on these questions will not be new; it has probably occurred to most scientists in one form or another. My principal aim is to illuminate it from several sides. The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.
Second, it is just this uncanny usefulness of mathematical concepts that raises the question of the uniqueness of our physical theories. In order to establish the first point, that mathematics plays an unreasonably important role in physics, it will be useful to say a few words on the question, “What is mathematics?”, then, “What is physics?”, then, how mathematics enters physical theories, and last, why the success of mathematics in its role in physics appears so baffling. Much less will be said on the second point: the uniqueness of the theories of physics. A proper answer to this question would require elaborate experimental and theoretical work which has not been undertaken to date.
I would say that mathematics is the science of skillful operations with concepts and rules invented just for this purpose. The principal emphasis is on the invention of concepts. Mathematics would soon run out of interesting theorems if these had to be formulated in terms of the concepts which already appear in the axioms. Furthermore, whereas it is unquestionably true that the concepts of elementary mathematics and particularly
elementary geometry were formulated to describe entities which are directly suggested by the actual world, the same does not seem to be true of the more advanced concepts, in particular the concepts which play such an important role in physics. Thus, the rules for operations with pairs of numbers are obviously designed to give the same results as the operations with fractions which we first learned without reference to “pairs of numbers.” The rules for the operations with sequences, that is, with irrational numbers, still belong to the category of rules which were determined so as to reproduce rules for the operations with quantities which were already known to us. Most more advanced mathematical concepts, such as complex numbers, algebras, linear operators, Borel sets, and this list could be continued almost indefinitely, were so devised that they are apt subjects on which the mathematician can demonstrate his ingenuity and sense of formal beauty. In fact, the definition of these concepts, with a realization that interesting and ingenious considerations could be applied to them, is the first demonstration of the ingeniousness of the mathematician who defines them. The depth of thought which goes into the formulation of the mathematical concepts is later justified by the skill with which these
concepts are used. The great mathematician fully, almost ruthlessly, exploits the domain of
permissible reasoning and skirts the impermissible. That his recklessness does not lead him into a morass of contradictions is a miracle in itself: certainly it is hard to believe that our reasoning power was brought, by Darwin’s process of natural selection, to the perfection which it seems to possess. However, this is not our present subject. The principal point which will have to be recalled later is that the mathematician could formulate only a handful of interesting theorems without defining concepts beyond those contained in the axioms and that the concepts outside those contained in the axioms are defined with a view of permitting ingenious logical operations which appeal to our aesthetic sense both as operations and also in their results of great generality.
Polanyi, in his Personal Knowledge (Chicago: University of Chicago Press, 1958), says: “All these difficulties are but consequences of our refusal to see that mathematics cannot be defined without acknowledging its most obvious feature: namely, that it is interesting” (p 188).
Certainly, nothing in our experience suggests the introduction of these quantities. Indeed, if a mathematician is asked to justify his interest in complex numbers, he will point, with some indignation, to the many beautiful theorems in the theory of equations, of power series, and of analytic functions in general, which owe their origin to the introduction of complex numbers. The mathematician is not willing to give up his interest in these most beautiful accomplishments of his genius.
The physicist is interested in discovering the laws of inanimate nature. In order to understand this statement, it is necessary to analyze the concept, “law of nature.” The world around us is of baffling complexity and the most obvious fact about it is that we cannot predict the future. Although the joke attributes only to the optimist the view that the future is uncertain, the optimist is right in this case: the future is unpredictable. It is, as Schrodinger has remarked, a miracle that in spite of the baffling complexity of the world, certain regularities in the events could be discovered. One such regularity, discovered by Galileo, is that two rocks, dropped at the same time from the same height, reach the ground at the same time. The laws of nature are concerned with such regularities. Galileo’s regularity is a prototype of a large class of regularities. It is a surprising regularity for three reasons.
The first reason that it is surprising is that it is true not only in Pisa, and in Galileo’s time,
it is true everywhere on the Earth, was always true, and will always be true. This property
of the regularity is a recognized invariance property and, as I had occasion to point out some time ago, without invariance principles similar to those implied in the preceding generalization of Galileo’s observation, physics would not be possible. The second surprising feature is that the regularity which we are discussing is independent of so many conditions which could have an effect on it. It is valid no matter whether it rains or not, whether the experiment is carried out in a room or from the Leaning Tower, no matter whether the person who drops the rocks is a man or a woman. It is valid even if the two rocks are dropped, simultaneously and from the same height, by two different people. There are, obviously, innumerable other conditions which are all immaterial from the point of view of the validity of Galileo’s regularity. The irrelevancy of so many circumstances which could play a role in the phenomenon observed has also been called an invariance. However, this invariance is of a different character from the preceding one since it cannot be formulated as a general principle. The exploration of the conditions which do, and which do not, influence a phenomenon is part of the early experimental exploration of a field. It is the skill and ingenuity of the experimenter which show him phenomena which depend on a relatively narrow set of relatively easily realizable and reproducible conditions. In the present case, Galileo’s restriction of his observations to relatively heavy bodies was the most important step in this regard. Again, it is true that if there were no phenomena which are independent of all but a manageably small set of conditions, physics would be impossible.
The preceding two points, though highly significant from the point of view of the philosopher, are not the ones which surprised Galileo most, nor do they contain a specific law of nature. The law of nature is contained in the statement that the length of time which it takes for a heavy object to fall from a given height is independent of the size, material, and shape of the body which drops. In the framework of Newton’s second “law,” this amounts to the statement that the gravitational force which acts on the falling body is proportional to its mass but independent of the size, material, and shape of the body which falls.
In the present case, Galileo’s restriction of his observations to relatively heavy bodies was the most important step in this regard. Again, it is true that if there were no phenomena which are independent of all but a manageably small set of conditions, physics would be impossible.
The present writer had occasion some time ago, to call attention to the succession of layers of “laws of nature,” each layer containing more general and more encompassing laws than the previous one and its discovery constituting a deeper penetration into the structure of the universe than the layers recognized before. However, the point which is most significant in the present context is that all these laws of nature contain, in even their remotest consequences, only a small part of our knowledge of the inanimate world. All the laws of nature are conditional statements which permit a prediction of some future events on the basis of the knowledge of the present, except that some aspects of the present state of the world, in practice the overwhelming majority of the determinants of the present state of the world, are irrelevant from the point of view of the prediction.
As regards the present state of the world, such as the existence of the earth on which we live and on which Galileo’s experiments were performed, the existence of the sun and of all our surroundings, the laws of nature are entirely silent. It is in consonance with this, first, that the laws of nature can be used to predict future events only under exceptional circumstances when all the relevant determinants of the present state of the world are known. It is also in consonance with this that the construction of machines, the functioning of which he can foresee, constitutes the most spectacular accomplishment of the physicist. In these machines, the physicist creates a situation in which all the relevant coordinates are known so that the behavior of the machine can be predicted. Radars and nuclear reactors are examples of such machines.
The principal purpose of the preceding discussion is to point out that the laws of nature are all conditional statements and they relate only to a very small part of our knowledge of the world. Thus, classical mechanics, which is the best known prototype of a physical theory, gives the second derivatives of the positional coordinates of all bodies, on the basis of the knowledge of the positions, etc., of these bodies. It gives no information on the existence, the present positions, or velocities of these bodies. It should be mentioned, for the sake of accuracy, that we discovered about thirty years ago that even the conditional statements cannot be entirely precise: that the conditional statements are probability laws which enable us only to place intelligent bets on future properties of the inanimate world, based on the knowledge of the present state. They do not allow us to make categorical statements, not even categorical statements conditional on the present state of the world. The probabilistic nature of the “laws of nature” manifests itself in the case of machines also, and can be verified, at least in the case of nuclear reactors, if one runs them at very low power. However, the additional limitation of the scope of the laws of nature which follows from their probabilistic nature will play no role in the rest of the discussion.
Having refreshed our minds as to the essence of mathematics and physics, we should be in a better position to review the role of mathematics in physical theories. Naturally, we do use mathematics in everyday physics to evaluate the results of the laws of nature, to apply the conditional statements to the particular conditions which happen to prevail or happen to interest us. In order that this be possible, the laws of nature must already be formulated in mathematical language. However, the role of evaluating the consequences of already established theories is not the most important role of mathematics in physics.
Mathematics does play, however, also a more sovereign role in physics. This was already implied in the statement, made when discussing the role of applied mathematics, that the laws of nature must have been formulated in the language of mathematics to be an object for the use of applied mathematics. The statement that the laws of nature are written in the language of mathematics was properly made three hundred years ago;9 it is now more true than ever before. In order to show the importance which mathematical concepts possess in the formulation of the laws of physics, let us recall, as an example, the axioms of quantum mechanics as formulated, explicitly, by the great physicist, Dirac. There are two basic concepts in quantum mechanics: states and observables. The states are vectors in Hilbert space, the observables self-adjoint operators on these vectors. The possible values of the observations are the characteristic values of the operators but we had better stop here lest we engage in a listing of the mathematical concepts developed in the theory of linear operators.
See: http://www.hep.upenn.edu/~johnda/Papers/wignerUnreasonableEffectiveness.pdf
Eugene Wigner, in full Eugene Paul Wigner, Hungarian Jenó Pál Wigner, (born November 17, 1902, Budapest, Hungary, Austria-Hungary—died January 1, 1995, Princeton, New Jersey, U.S.), Hungarian-born American physicist, joint winner, with J. Hans D. Jensen of West Germany and Maria Goeppert Mayer of the United States, of the Nobel Prize for Physics in 1963.
He received the prize for his many contributions to nuclear physics, which include his formulation of the law of conservation of parity.
Wigner studied chemical engineering and received a Ph.D. from the Institute of Technology in Berlin in 1925. After serving as a lecturer there and at the University of Göttingen, he emigrated to the United States.
Apart from two years (1936–38) as professor of physics at the University of Wisconsin, he spent his academic life at Princeton University, serving as a professor of mathematical physics from 1938 until his retirement in 1971. He became a naturalized U.S. citizen in 1937.
See: https://www.britannica.com/biography/Eugene-Wigner
Wigner is telling us , first, that it is not at all natural that “laws of nature” exist, much less that man is able to discover them. He is also explains that mathematics, or, rather, applied mathematics, is not so much the master of the situation in this function: it is merely serving as a tool. A tool to explain the natural processes unfolding in the universe.
Hartmann352
Attachments
100 yrs. of math have failed to discern the source of atomic patterns. Math gives you point entities with innate properties and they call this science. I have a different word for it. It's pathetic and Einstein, with many others, warned us about attempting this 100 years ago.
Do you believe that the pattern that was emitted, is the same atomic pattern when not emitting?
Do you believe that the atomic pattern is the same at steady state, absorption and emission, and all have the same pattern? Do you believe that there is any physical change in an atom......during these events? Is the pattern, a pattern of the atom, OR is the pattern, only the CHANGE or a DIFFERENCE of the atomic pattern? A transition pattern? How much of the inducing pattern is passed to the emission pattern?
Is "mass", the only thing that changes during absorption and emission? How about accelerating a particle, is mass, the only property that changes? The frequency of the spin, also increases with a gain in mass. The frequency of the spin, decreases during emission. But the velocity of the spin remains constant. How can that be....and what does that mean? It means the the circumference of the spin, has to be decreased to increase spin frequency(RPM) and increased to decrease the RPM, while keeping the spin velocity constant. This means that the particle changes size too, with energy/mass levels. That means the EM field densities change with mass. The mass is inertia. And the inertia changes with field density and RPM. Density and RPM IS the mass/inertia of a particle.
All of these changes are in quantum steps. These steps are not analog and they are not uniform. Uneven and seemingly unrelated with no common pattern. It's sorta like a staircase with random step heights. Math can find a common number of any set....so what....that's the way numbers work.
All of this will lead to very complex patterns, especially if you have no bases to start from. It's a super puzzle. I love it. Only one other puzzle is greater, but requires you to die to solve it.
And we ain't done yet. What about the measurement of these patterns? We induce with a force that we know that the atom will react to. A sensitive force.
So, when we detect that pattern, does the reaction of the detector......add to the detected pattern? How much of the pattern that we detect, is from the atom and how much is from the detection of the pattern?
Using math for a guide will give us another 100 yrs. of this puzzle.
The physical model I use solves much more than just defining "mass". It describes the physical dynamic of emission, propagation and absorption. It physically describes dipoles and their bonds and nuclei and their bonds. It physically explains anti matter. It describes what neutrons are and how there are made and why they fall apart. It will physically explain the weak and asymmetric force of gravity.
It's a physical model of physicality. It can not explain how, when or where, or WHY physicality came to be. It can not explain life or other super natural(thought and math) concepts. It can not explain death and thereafter. Or why life is. Or why matter is.
But it does exhibit the absence of randomness, chaos, probability, information and math. It does show a universe with absolute time and length. The pillars of physicality are firm and square. It truly is rock solid. We exist in a universe of perfection and elegance. And no one knows it. An irony within an irony. And nature chuckles on.
If you use numbers to quantify everything, then everything has a math relationship.
Come on, man.
Do you believe that the pattern that was emitted, is the same atomic pattern when not emitting?
Do you believe that the atomic pattern is the same at steady state, absorption and emission, and all have the same pattern? Do you believe that there is any physical change in an atom......during these events? Is the pattern, a pattern of the atom, OR is the pattern, only the CHANGE or a DIFFERENCE of the atomic pattern? A transition pattern? How much of the inducing pattern is passed to the emission pattern?
Is "mass", the only thing that changes during absorption and emission? How about accelerating a particle, is mass, the only property that changes? The frequency of the spin, also increases with a gain in mass. The frequency of the spin, decreases during emission. But the velocity of the spin remains constant. How can that be....and what does that mean? It means the the circumference of the spin, has to be decreased to increase spin frequency(RPM) and increased to decrease the RPM, while keeping the spin velocity constant. This means that the particle changes size too, with energy/mass levels. That means the EM field densities change with mass. The mass is inertia. And the inertia changes with field density and RPM. Density and RPM IS the mass/inertia of a particle.
All of these changes are in quantum steps. These steps are not analog and they are not uniform. Uneven and seemingly unrelated with no common pattern. It's sorta like a staircase with random step heights. Math can find a common number of any set....so what....that's the way numbers work.
All of this will lead to very complex patterns, especially if you have no bases to start from. It's a super puzzle. I love it. Only one other puzzle is greater, but requires you to die to solve it.
And we ain't done yet. What about the measurement of these patterns? We induce with a force that we know that the atom will react to. A sensitive force.
So, when we detect that pattern, does the reaction of the detector......add to the detected pattern? How much of the pattern that we detect, is from the atom and how much is from the detection of the pattern?
Using math for a guide will give us another 100 yrs. of this puzzle.
The physical model I use solves much more than just defining "mass". It describes the physical dynamic of emission, propagation and absorption. It physically describes dipoles and their bonds and nuclei and their bonds. It physically explains anti matter. It describes what neutrons are and how there are made and why they fall apart. It will physically explain the weak and asymmetric force of gravity.
It's a physical model of physicality. It can not explain how, when or where, or WHY physicality came to be. It can not explain life or other super natural(thought and math) concepts. It can not explain death and thereafter. Or why life is. Or why matter is.
But it does exhibit the absence of randomness, chaos, probability, information and math. It does show a universe with absolute time and length. The pillars of physicality are firm and square. It truly is rock solid. We exist in a universe of perfection and elegance. And no one knows it. An irony within an irony. And nature chuckles on.
If you use numbers to quantify everything, then everything has a math relationship.
Come on, man.
First, I thank you for your erudite responses. I learn something new every time I read your missives. Consider my arguments as probative rather than definitive.
Seems to me that the generic mathematical logic is functional under similar conditions of similar relational values.
IMO, the universe does not deal so much with numbers as it deals with relational values, whatever they may be, but can be symbolically approximated with human codified value systems.
I like this article.
Why Math is the "Language of the Universe:"
The symbolic nature of representative mathematics may change but not the inherent logical processes.
Interestingly, Ricky Gervais made this elegant argument that, if we were to burn all scripture and all mathematical scientific literature today and tried to duplicate both 500 years from now, all scripture would be different from today, yet all the mathematics would be exactly the same as they are today.

 futurism.com
futurism.com
In the example, the question should ask if both are mathematical patterns, even if they differ in behavior and no equation can be formulated.
My question is not if mathematics creates regular patterns, but if regular patterns are all mathematically (logically) organized.
I believe the Table of Elements speaks eloquently in favor of mathematical patterns emerging from dynamical and chaotic fundamental particle fields, as described in Chaos Theory.
But cosmologists insist that the mathematics of the universe are not just conceptual, but are the result of observation of the appearance of certain regularities when conditions consist of similar values.I would say that mathematics is the science of skilful operations with concepts and rules invented just for this purpose. The principal emphasis is on the invention of concepts. Mathematics would soon run out of interesting theorems if these had to be formulated in terms of the concepts which already appear in the axioms.
But you are speaking in mathematical terms. I am not arguing for human maths. Human mathematics is a codified system of symbolic representation of the interactive behaviors of generic relational values that create unique or recurring patterns, i.e. a form of generic mathematical processes.Furthermore, whereas it is unquestionably true that the concepts of elementary mathematics and particularly elementary geometry were formulated to describe entities which are directly suggested by the actual world, the same does not seem to be true of the more advanced concepts, in particular the concepts which play such an important role in physics. Thus, the rules for operations with pairs of numbers are obviously designed to give the same results as the operations with fractions which we first learned without reference to “pairs of numbers.”
Am I correct in equating the irrational number of "pi" with its "rational" application to circles from infinitely small to infinitely big?The rules for the operations with sequences, that is, with irrational numbers, still belong to the category of rules which were determined so as to reproduce rules for the operations with quantities which were already known to us.
Seems to me that the generic mathematical logic is functional under similar conditions of similar relational values.
IMO, the universe does not deal so much with numbers as it deals with relational values, whatever they may be, but can be symbolically approximated with human codified value systems.
I like this article.
Why Math is the "Language of the Universe:"
I totally agree. It is an essential property of spacetime geometry.To start with, Mathematics does not have a clearly defined, universally accepted definition. However it is safe to say that anything that studies the interaction between quantities, variables, structure, and change, is mathematics. Mathematics is not a tangible thing, but actually an abstract concept.
Here is where I disagree.Other civilizations have made other ways of expressing mathematics, and if we ever run into alien intelligence, it is likely that they will use a different system than we do.
The symbolic nature of representative mathematics may change but not the inherent logical processes.
Interestingly, Ricky Gervais made this elegant argument that, if we were to burn all scripture and all mathematical scientific literature today and tried to duplicate both 500 years from now, all scripture would be different from today, yet all the mathematics would be exactly the same as they are today.
But the system is not the thing. This is because mathematics is the expression and quantification of basic logical concepts, and then it builds on those logical concepts to form increasingly complex concepts. It is, however, entirely a logical progression.
The confusing thing is that even though absolute logical proof is impossible as per Münchhausen’s Trilemma, it is still usually pretty easy to determine if a logical thread is valid or not, particularly in mathematics.
Mathematics is the most fundamental type of logic possible (in physics anyway), and therefore it is easy to reason that mathematics is the best way of expressing the universe.
But if we choose to ignore the murky waters of elementary logic, mathematics becomes the language of the universe simply because it has to be.
There is no simpler, more fundamental way of expressing the universe than through the basic ideas of equality and inequality, which in turn lead to the concept of quantification, which lead to the concept of value and numbers (to expressed levels of inequality), and once we have numbers, the rest of mathematics seems to bloom from all around us.
But again, the system we use to describe mathematics and mathematics itself are two completely different things.

Why Math is the "Language of the Universe:"
Question: I’ve always wondered why is it mathematics is considered the "universal language" in physics and the explanation of the natural world. What is the possibility of different civilizations (here on earth) and different life forms (else where in the cosmos) using some other complex...
imho, that is not a valid question.Do you believe that the pattern that was emitted, is the same atomic pattern when not emitting?
In the example, the question should ask if both are mathematical patterns, even if they differ in behavior and no equation can be formulated.
My question is not if mathematics creates regular patterns, but if regular patterns are all mathematically (logically) organized.
I believe the Table of Elements speaks eloquently in favor of mathematical patterns emerging from dynamical and chaotic fundamental particle fields, as described in Chaos Theory.
Last edited:
write4u, here are some ideas on mathematics you might want to consider when you speak of mathematical patterns.
Mathematics is derived from the contributions of thinkers throughout the ages and across the globe. It gives us a way to understand patterns, to quantify relationships, and to predict the future. Math helps us understand the world — and we use the world to understand math.
The world is interconnected. Everyday math shows these connections and possibilities.
Algebra can explain how quickly water becomes contaminated and how many people in a third-world country drinking that water might become sickened on a yearly basis. A study of geometry can explain the science behind architecture throughout the world. Statistics and probability can estimate death tolls from earthquakes, conflicts and other calamities around the world. It can also predict profits, how ideas spread, and how previously endangered animals might repopulate. Math is a powerful tool for global understanding and communication. Using it, students can make sense of the world and solve complex and real problems. Rethinking math in a global context offers students a twist on the typical content that makes the math itself more applicable and meaningful for students.
For all of us to function in a global context, math content needs to help us get to global competence, which is understanding different perspectives and world conditions, recognizing that issues are interconnected across the globe, as well as communicating and acting in appropriate ways. In math, this means reconsidering the typical content in atypical ways, and explaining how the world consists of situations, events and phenomena that can be sorted out using the right math tools.
Math is often studied as a pure science, but is typically applied to other disciplines, extending well beyond physics and engineering. For instance, studying exponential growth and decay (the rate at which things grow and die) within the context of population growth, the spread of disease, or water contamination, is meaningful. It not only gives us a real-world context in which to use the math, but helps us understand global phenomena – a disease spreading in India, but we can’t make the connection without understanding how fast something like cholera can spread in a dense population. In fact, adding a study of growth and decay to lower level algebra – it’s most often found in algebra II – may give us a chance to study it in the global context than if it’s reserved for the upper level math that not all students take.
In a similar vein, a study of statistics and probability is key to understanding many of the events of the world, and is usually reserved for students at a higher level of math, if it gets any study in high school at all. But many world events and phenomena are unpredictable and can only be described using statistical models, so a globally focused math program needs to consider including statistics. Probability and statistics can be used to estimate death tolls from natural disasters, such as earthquakes and tsunamis; the amount of aid that might be necessary to help in the aftermath; and the number people who would be displaced.
Understanding the world also means appreciating the contributions of other cultures. In algebra, students could benefit from studying numbers systems that are rooted in other cultures, such the Mayan and Babylonian systems, a base 20 and base 60 system, respectively. They gave us elements that still work in current math systems, such as the 360 degrees in a circle, and the division of the hour into 60 minute intervals, and including this type of content can help develop an appreciation for the contributions other cultures have made to our understanding of math.
Mathematics is all about numbers. It involves the study of different patterns. And there are different types of patterns, such as number patterns, image patterns, logic patterns, word patterns etc. Number patterns are very common in Mathematics. These are quite familiar to the students who study Maths frequently. Especially, number patterns are everywhere in Mathematics. Number patterns are all predictions. In this article, we will discuss what is a pattern, and different types of patterns like, arithmetic pattern, geometric pattern and many solved examples.
In Mathematics, a pattern is a repeated arrangement of numbers, shapes, colours and so on. The Pattern can be related to any type of event or object. If the set of numbers are related to each other in a specific rule, then the rule or manner is called a pattern. Sometimes, patterns are also known as a sequence. Patterns are finite or infinite in numbers.
For example, in a sequence 2,4,6,8,?. each number is increasing by sequence 2. So, the last number will be 8 + 2 = 10.
Few examples of numerical patterns are:
Even numbers pattern -: 2, 4, 6, 8, 10, 1, 14, 16, 18, …
Odd numbers pattern -: 3, 5, 7, 9, 11, 13, 15, 17, 19, …
Fibonacci numbers pattern -: 1, 1, 2, 3, 5, 8 ,13, 21, … and so on.
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
For example, 2, 4, 6, 8, 10, __, 14, __. Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 2 to the previous term to get the next term”.
In the example given above, take the second term (4). If we add “2” to the second term (4), we get the third term 6.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 10. Therefore, 10+2 = 12.
Second missing term: The previous term is 14. So, 14+2 = 16
Hence, the complete arithmetic pattern is 2, 4, 6, 8, 10, 12, 14, 16.
The geometric pattern is defined as the sequence of numbers that are based on the multiplication and division operation. Similar to the arithmetic pattern, if two or more numbers in the sequence are provided, we can easily find the unknown terms in the pattern using multiplication and division operation.
For example, 8, 16, 32, __, 128, __.
It is a geometric pattern, as each term in the sequence can be obtained by multiplying 2 with the previous term.
For example, 32 is the third term in the sequence, which is obtained by multiplying 2 with the previous term 16.
Likewise, we can find the unknown terms in the geometric pattern.
First missing term: The previous term is 32. Multiply 32 by 2, we get 64.
Second missing term: The previous term is 128. Multiply 128 by 2, we get 256.
Hence, the complete geometric pattern is 8, 16, 32, 64, 128, 256.
The Fibonacci Pattern is defined as the sequence of numbers, in which each term in the sequence is obtained by adding the two terms before it, starting with the numbers 0 and 1. The Fibonacci pattern is given as 0, 1, 1, 2, 3, 5, 8, 13, … and so on.
Third term = First term + Second term = 0+1 = 1
Fourth term = second term + Third term = 1+1 = 2
Fifth term = Third term + Fourth term = 1+2 = 3, and so on.
To construct a pattern, we have to know about some rules. To know about the rule for any pattern, we have to understand the nature of the sequence and the difference between the two successive terms.
Finding Missing Term: Consider a pattern 1, 4, 9, 16, 25, ?. In this pattern, it is clear that every number is the square of their position number. The missing term takes place at n = 6. So, if the missing is xn, then xn = n2. Here, n = 6, then xn = (6)2 = 36.
Difference Rule: Sometimes, it is easy to find the difference between two successive terms. For example, consider 1, 5, 9, 13,……. In this type of pattern, first, we have to find the difference between two pairs of the sequence. After that, find the remaining elements of the pattern. In the given problem, the difference between the terms is 4, i.e.if we add 4 and 1, we get 5, and if we add 4 and 5, we get 9 and so on.
In Discrete Mathematics, we have three types of patterns as follows:
Patterns provide a sense of order in what might otherwise appear chaotic. When you notice that things happen in a certain pattern - even something as mundane as a bus always stopping at a certain corner at 5pm - order is provided.
Patterns allow someone to make educated guesses. Much science is based on making a hypothesis and hypothoses are often based on understanding patterns. Similarly, we make many common assumptions based on recurring patterns.
Understanding patterns aid in developing mental skills. In order to recognize patterns one need to have an understanding of critical thinking and logic and these are clearly important skills to develop.
Patterns can provide a clear understanding of mathematical relationships. This can be seen in a very evident manner in the form of multiplication tables. 2 x2, 2 x 4, 2 x 6 are clearly examples of the relationship pattern found in multiplication.
Understanding patterns can provide the basis for understanding algebra. This is because a major component of solving algebra problems involves data analysis which is deeply related to the understanding of patterns. Without being able to recognize the appearance of patterns the ability to be proficient in algebra will be limited.
Understanding patterns provide a clear basis for problem solving skills. In a way, this is related to critical thinking but more directed towards mathematics specifically. Patterns essentially provide a means of recognizing the broader aspects that can be shored down in order to arrive at the specific answer to a particular problem.
Knowledge of patterns is transferred into science fields where they prove very helpful. Understanding animal patterns has been used to help endangered species. Understanding weather patterns not only allows one to predict the weather but also predict the common impact of weather which can aid in devising the appropriate response in an emergency situation.
One of the lesser known aspects of patterns is the fact that they often form the basis of music. For example, there are various patterns of notes that provide the basis for proper harmony on a piano. If you don't believe patterns are important when playing a piano simply walk up to the nearest piano and start banging away randomly at the keys. You probably won't hear any songs that you recognize!
Patterns provide clear insight into the natural world. While animals and certainly plants are far from thinking beings they do have certain habits that exist in patterns and understanding these behavioral patterns provides a clearer understanding of all living things.
It is safe to say that the benefits of understanding patterns open many doors where this knowledge can be applied. Of course, that is a commonality with all forms of learning mathematical logic: there is a deep application that can be provided that we often do not realize when we first study the material. With understanding patterns - and other forms of math - sometimes you really need to stick with it for the long term, but with that practice comes skill. Researchers have found that pattern skills can be learned relatively quickly.
Regular expression patterns can capture simple but com- mon and important properties easily, even though they are not as powerful as languages in more sophisticated frame- works. The combined power and simplicity of regular ex- pressions contribute to their wide use in computing, from languages and compilers, to database and web information retrieval, to operating systems and security, etc.
Parametric regular path queries extend the patterns with variables, called parameters, which significantly increase the expressiveness by allowing additional information along sin- gle or multiple paths to be captured and related, and the amount of such information is not bounded by the size of the pattern. This extension enables analysis of significantly many more important properties about dependencies, con- currency, resource usage, etc. The regular expression pat- terns used to analyze these properties are simple, easy to write, and succinct.
General algorithms have been studied for solving simpler regular path queries, in particular, queries involving uncor- related paths and queries containing no variables. A method was also proposed to code parametric regular path queries using logic programs. What have been lacking are complete algorithms and data structures for solving parametric regular path queries directly, efficiently, and with precise complexity analysis.
See: https://byjus.com/maths/patterns/
See: https://www.mathworksheetscenter.com/mathtips/mathpatterns.html
See: https://asiasociety.org/education/understanding-world-through-math
Getting back to Max Tegmark again...
In an article entitled “Parallel Universes” in the May 2003 issue of Scientific American (https://www.scientificamerican.com/magazine/sa/2003/05-01/), Tegmark presents a clear and comprehensive picture of the parallel-universe idea. What Tegmark describes is actually a set of related concepts which have in common the notion that there are universes beyond the familiar observable one that astronomers can see parts of directly with telescopes and other instruments. Some of these parallel universes are completely unlike our own; others are nearly identical; still others are identical up to a point and then split off into might-have-been worlds of choices not made.
Tegmark’s main argument is that, far from being a shadowy, speculative corner of cosmology, the parallel-universe idea has been increasingly confirmed by recent experiments, and we should get used to it because it appears that it will be around for a while.
If true, this is not good news for proponents of intelligent design such as William A. Dembski. In his recent book No Free Lunch, Dembski is at considerable pains to show why the parallel-universe idea is basically a non-starter. He recognizes the threat that parallel universes pose to the concept of specified complexity. Simply expressed, if literally anything can happen, it will, including the most unlikely and designed-looking things such as earth, life, and humanity. If certain forms of the parallel-universe idea are true, then chance, not design, becomes omnipotent.
Cosmology has always bordered upon metaphysics. Questions of ultimate origin and destiny began as metaphysical questions, and only in the last century has science begun seriously to address some of these issues with theories based on empirical evidence. It is still not always easy, therefore, to distinguish cosmology based on empirical evidence from a philosophical position disguised as empirical cosmology. Tegmark’s article deals largely with theories whose main feature, namely, multiple universes, cannot be verified by observation or experiment even in principle. The experimental tests he proposes for these theories really consist in making the philosophical presuppositions required for believing in the theories, and then verifying that the theories agree with already-known data about the present visible universe. So far from being a legitimate way to inflate probabilistic resources to defeat arguments in favor of intelligent design, Tegmark’s parallel universes represent an array of philosophical arguments disguised as science. While the philosophical arguments may have merit on their own, it is illegitimate to claim that they are empirically verified in the conventional scientific sense, as Tegmark sometimes does.
Hartmann352
Mathematics is derived from the contributions of thinkers throughout the ages and across the globe. It gives us a way to understand patterns, to quantify relationships, and to predict the future. Math helps us understand the world — and we use the world to understand math.
The world is interconnected. Everyday math shows these connections and possibilities.
Algebra can explain how quickly water becomes contaminated and how many people in a third-world country drinking that water might become sickened on a yearly basis. A study of geometry can explain the science behind architecture throughout the world. Statistics and probability can estimate death tolls from earthquakes, conflicts and other calamities around the world. It can also predict profits, how ideas spread, and how previously endangered animals might repopulate. Math is a powerful tool for global understanding and communication. Using it, students can make sense of the world and solve complex and real problems. Rethinking math in a global context offers students a twist on the typical content that makes the math itself more applicable and meaningful for students.
For all of us to function in a global context, math content needs to help us get to global competence, which is understanding different perspectives and world conditions, recognizing that issues are interconnected across the globe, as well as communicating and acting in appropriate ways. In math, this means reconsidering the typical content in atypical ways, and explaining how the world consists of situations, events and phenomena that can be sorted out using the right math tools.
Math is often studied as a pure science, but is typically applied to other disciplines, extending well beyond physics and engineering. For instance, studying exponential growth and decay (the rate at which things grow and die) within the context of population growth, the spread of disease, or water contamination, is meaningful. It not only gives us a real-world context in which to use the math, but helps us understand global phenomena – a disease spreading in India, but we can’t make the connection without understanding how fast something like cholera can spread in a dense population. In fact, adding a study of growth and decay to lower level algebra – it’s most often found in algebra II – may give us a chance to study it in the global context than if it’s reserved for the upper level math that not all students take.
In a similar vein, a study of statistics and probability is key to understanding many of the events of the world, and is usually reserved for students at a higher level of math, if it gets any study in high school at all. But many world events and phenomena are unpredictable and can only be described using statistical models, so a globally focused math program needs to consider including statistics. Probability and statistics can be used to estimate death tolls from natural disasters, such as earthquakes and tsunamis; the amount of aid that might be necessary to help in the aftermath; and the number people who would be displaced.
Understanding the world also means appreciating the contributions of other cultures. In algebra, students could benefit from studying numbers systems that are rooted in other cultures, such the Mayan and Babylonian systems, a base 20 and base 60 system, respectively. They gave us elements that still work in current math systems, such as the 360 degrees in a circle, and the division of the hour into 60 minute intervals, and including this type of content can help develop an appreciation for the contributions other cultures have made to our understanding of math.
Mathematics is all about numbers. It involves the study of different patterns. And there are different types of patterns, such as number patterns, image patterns, logic patterns, word patterns etc. Number patterns are very common in Mathematics. These are quite familiar to the students who study Maths frequently. Especially, number patterns are everywhere in Mathematics. Number patterns are all predictions. In this article, we will discuss what is a pattern, and different types of patterns like, arithmetic pattern, geometric pattern and many solved examples.
In Mathematics, a pattern is a repeated arrangement of numbers, shapes, colours and so on. The Pattern can be related to any type of event or object. If the set of numbers are related to each other in a specific rule, then the rule or manner is called a pattern. Sometimes, patterns are also known as a sequence. Patterns are finite or infinite in numbers.
For example, in a sequence 2,4,6,8,?. each number is increasing by sequence 2. So, the last number will be 8 + 2 = 10.
Few examples of numerical patterns are:
Even numbers pattern -: 2, 4, 6, 8, 10, 1, 14, 16, 18, …
Odd numbers pattern -: 3, 5, 7, 9, 11, 13, 15, 17, 19, …
Fibonacci numbers pattern -: 1, 1, 2, 3, 5, 8 ,13, 21, … and so on.
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
For example, 2, 4, 6, 8, 10, __, 14, __. Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 2 to the previous term to get the next term”.
In the example given above, take the second term (4). If we add “2” to the second term (4), we get the third term 6.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 10. Therefore, 10+2 = 12.
Second missing term: The previous term is 14. So, 14+2 = 16
Hence, the complete arithmetic pattern is 2, 4, 6, 8, 10, 12, 14, 16.
The geometric pattern is defined as the sequence of numbers that are based on the multiplication and division operation. Similar to the arithmetic pattern, if two or more numbers in the sequence are provided, we can easily find the unknown terms in the pattern using multiplication and division operation.
For example, 8, 16, 32, __, 128, __.
It is a geometric pattern, as each term in the sequence can be obtained by multiplying 2 with the previous term.
For example, 32 is the third term in the sequence, which is obtained by multiplying 2 with the previous term 16.
Likewise, we can find the unknown terms in the geometric pattern.
First missing term: The previous term is 32. Multiply 32 by 2, we get 64.
Second missing term: The previous term is 128. Multiply 128 by 2, we get 256.
Hence, the complete geometric pattern is 8, 16, 32, 64, 128, 256.
The Fibonacci Pattern is defined as the sequence of numbers, in which each term in the sequence is obtained by adding the two terms before it, starting with the numbers 0 and 1. The Fibonacci pattern is given as 0, 1, 1, 2, 3, 5, 8, 13, … and so on.
Third term = First term + Second term = 0+1 = 1
Fourth term = second term + Third term = 1+1 = 2
Fifth term = Third term + Fourth term = 1+2 = 3, and so on.
To construct a pattern, we have to know about some rules. To know about the rule for any pattern, we have to understand the nature of the sequence and the difference between the two successive terms.
Finding Missing Term: Consider a pattern 1, 4, 9, 16, 25, ?. In this pattern, it is clear that every number is the square of their position number. The missing term takes place at n = 6. So, if the missing is xn, then xn = n2. Here, n = 6, then xn = (6)2 = 36.
Difference Rule: Sometimes, it is easy to find the difference between two successive terms. For example, consider 1, 5, 9, 13,……. In this type of pattern, first, we have to find the difference between two pairs of the sequence. After that, find the remaining elements of the pattern. In the given problem, the difference between the terms is 4, i.e.if we add 4 and 1, we get 5, and if we add 4 and 5, we get 9 and so on.
In Discrete Mathematics, we have three types of patterns as follows:
- Repeating – A type of pattern, in which the rule keeps repeating over and over is called a repeating pattern.
- Growing – If the numbers are present in the increasing form, then the pattern is known as a growing pattern. Example 34, 40, 46, 52, …..
- Shirking – In the shirking pattern, the numbers are in decreasing form. Example: 42, 40, 38, 36 …..
Patterns provide a sense of order in what might otherwise appear chaotic. When you notice that things happen in a certain pattern - even something as mundane as a bus always stopping at a certain corner at 5pm - order is provided.
Patterns allow someone to make educated guesses. Much science is based on making a hypothesis and hypothoses are often based on understanding patterns. Similarly, we make many common assumptions based on recurring patterns.
Understanding patterns aid in developing mental skills. In order to recognize patterns one need to have an understanding of critical thinking and logic and these are clearly important skills to develop.
Patterns can provide a clear understanding of mathematical relationships. This can be seen in a very evident manner in the form of multiplication tables. 2 x2, 2 x 4, 2 x 6 are clearly examples of the relationship pattern found in multiplication.
Understanding patterns can provide the basis for understanding algebra. This is because a major component of solving algebra problems involves data analysis which is deeply related to the understanding of patterns. Without being able to recognize the appearance of patterns the ability to be proficient in algebra will be limited.
Understanding patterns provide a clear basis for problem solving skills. In a way, this is related to critical thinking but more directed towards mathematics specifically. Patterns essentially provide a means of recognizing the broader aspects that can be shored down in order to arrive at the specific answer to a particular problem.
Knowledge of patterns is transferred into science fields where they prove very helpful. Understanding animal patterns has been used to help endangered species. Understanding weather patterns not only allows one to predict the weather but also predict the common impact of weather which can aid in devising the appropriate response in an emergency situation.
One of the lesser known aspects of patterns is the fact that they often form the basis of music. For example, there are various patterns of notes that provide the basis for proper harmony on a piano. If you don't believe patterns are important when playing a piano simply walk up to the nearest piano and start banging away randomly at the keys. You probably won't hear any songs that you recognize!
Patterns provide clear insight into the natural world. While animals and certainly plants are far from thinking beings they do have certain habits that exist in patterns and understanding these behavioral patterns provides a clearer understanding of all living things.
It is safe to say that the benefits of understanding patterns open many doors where this knowledge can be applied. Of course, that is a commonality with all forms of learning mathematical logic: there is a deep application that can be provided that we often do not realize when we first study the material. With understanding patterns - and other forms of math - sometimes you really need to stick with it for the long term, but with that practice comes skill. Researchers have found that pattern skills can be learned relatively quickly.
Regular expression patterns can capture simple but com- mon and important properties easily, even though they are not as powerful as languages in more sophisticated frame- works. The combined power and simplicity of regular ex- pressions contribute to their wide use in computing, from languages and compilers, to database and web information retrieval, to operating systems and security, etc.
Parametric regular path queries extend the patterns with variables, called parameters, which significantly increase the expressiveness by allowing additional information along sin- gle or multiple paths to be captured and related, and the amount of such information is not bounded by the size of the pattern. This extension enables analysis of significantly many more important properties about dependencies, con- currency, resource usage, etc. The regular expression pat- terns used to analyze these properties are simple, easy to write, and succinct.
General algorithms have been studied for solving simpler regular path queries, in particular, queries involving uncor- related paths and queries containing no variables. A method was also proposed to code parametric regular path queries using logic programs. What have been lacking are complete algorithms and data structures for solving parametric regular path queries directly, efficiently, and with precise complexity analysis.
See: https://byjus.com/maths/patterns/
See: https://www.mathworksheetscenter.com/mathtips/mathpatterns.html
See: https://asiasociety.org/education/understanding-world-through-math
Getting back to Max Tegmark again...
In an article entitled “Parallel Universes” in the May 2003 issue of Scientific American (https://www.scientificamerican.com/magazine/sa/2003/05-01/), Tegmark presents a clear and comprehensive picture of the parallel-universe idea. What Tegmark describes is actually a set of related concepts which have in common the notion that there are universes beyond the familiar observable one that astronomers can see parts of directly with telescopes and other instruments. Some of these parallel universes are completely unlike our own; others are nearly identical; still others are identical up to a point and then split off into might-have-been worlds of choices not made.
Tegmark’s main argument is that, far from being a shadowy, speculative corner of cosmology, the parallel-universe idea has been increasingly confirmed by recent experiments, and we should get used to it because it appears that it will be around for a while.
If true, this is not good news for proponents of intelligent design such as William A. Dembski. In his recent book No Free Lunch, Dembski is at considerable pains to show why the parallel-universe idea is basically a non-starter. He recognizes the threat that parallel universes pose to the concept of specified complexity. Simply expressed, if literally anything can happen, it will, including the most unlikely and designed-looking things such as earth, life, and humanity. If certain forms of the parallel-universe idea are true, then chance, not design, becomes omnipotent.
Cosmology has always bordered upon metaphysics. Questions of ultimate origin and destiny began as metaphysical questions, and only in the last century has science begun seriously to address some of these issues with theories based on empirical evidence. It is still not always easy, therefore, to distinguish cosmology based on empirical evidence from a philosophical position disguised as empirical cosmology. Tegmark’s article deals largely with theories whose main feature, namely, multiple universes, cannot be verified by observation or experiment even in principle. The experimental tests he proposes for these theories really consist in making the philosophical presuppositions required for believing in the theories, and then verifying that the theories agree with already-known data about the present visible universe. So far from being a legitimate way to inflate probabilistic resources to defeat arguments in favor of intelligent design, Tegmark’s parallel universes represent an array of philosophical arguments disguised as science. While the philosophical arguments may have merit on their own, it is illegitimate to claim that they are empirically verified in the conventional scientific sense, as Tegmark sometimes does.
Hartmann352
I agree.Math helps us understand the world — and we use the world to understand math.
I agree and mathematics hones those cognitive and logical skills.Understanding patterns aid in developing mental skills. In order to recognize patterns one need to have an understanding of critical thinking and logic and these are clearly important skills to develop.
I agree with everything you posit.
But none of it seems to falsify a mathematical universe, other
than chaos.
Can we say that logical mathematics is an emergent property of evolving systems?
I am not really all that interested in Tegmark's multiverse. That is way beyond my paygrade. But I am an ex-bookkeeper and I have come to appreciate the simple logical elegance of mathematically guided processing of relational values via logical interactive functions that result in the observable ordering of the physical world.
Mathematics are not object dependent. They are value dependent.
IMO, it is natural selection that favors those mathematical patterns that yield the greatest integral efficiency with the least expenditure of energy.
This is why nature favors the Fibonacci sequence in flora as it results in a symmetrical, well-balanced efficient structure that allows for vertical growth and offers the most efficient branching distribution of energy receptors in leaves, petals, and of maximum packing in seed distribution.
Plants do not know maths, but they use it everywhere!
That must be a genetic code, an evolved growth instruction that follows a sequence that we have codified as the Fibonacci sequence.
Why is it that bees create the extraordinary mathematically perfect honeycombs ? Natural selection.
It appears then that nature itself stochastically selects for mathematical order and regularity in a dynamical environment.
But once a pattern is able to self-organize into a complex set, that set tends to repeat especially. in living organisms and duplicating patterns.
And that should be observable, which it is!
The microtubule is perfect example of a self-organizing object that has become essential for the duplication of cells and the neural network that has acquired the conscious ability of cognition of abstract mathematical properties inherent in much, if not all manifest reality.
Nature has no need for human symbolisms, humans do.
As you posit, we need our maths to understand how the universe functions.
Last edited:
Similar threads
- Replies
- 3
- Views
- 361
- Replies
- 1
- Views
- 343
- Replies
- 1
- Views
- 359
- Replies
- 1
- Views
- 393
TRENDING THREADS
-
What is a living individual and is it naturally universally mobile?
- Started by tonylang
- Replies: 138

Live Science is part of Future plc, an international media group and leading digital publisher. Visit our corporate site.
© Future Publishing Limited Quay House, The Ambury, Bath BA1 1UA. All rights reserved. England and Wales company registration number 2008885.
