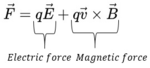This is a simple equation within what is called “Lorentz force equation”. This reason I pointed this out is that sometimes people confuse electrical fields and magnetic fields as being the same. This equation is used to figure out the force (F) of the combination of an electrical force (qE) and a magnetic force (qv + B) the changing direction.
An electrical field is the force per unit charge experienced by a non-moving point charge charge at any given point within that field. While a magnetic field is only detected by the force it exerts on other magnetic particles or electric charges.
In conclusion you have to have an electrical field that produces a magnetic field as a byproduct. They are two different fields and force vectors. Electrical fields can exist without a magnetic field a stationary point charge. A magnetic field cannot exist without an E field component because there are no magnetic monopoles they are always bi-poles a North Pole and a South Pole and the surface area is always equal to zero.
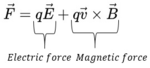
An electrical field is the force per unit charge experienced by a non-moving point charge charge at any given point within that field. While a magnetic field is only detected by the force it exerts on other magnetic particles or electric charges.
In conclusion you have to have an electrical field that produces a magnetic field as a byproduct. They are two different fields and force vectors. Electrical fields can exist without a magnetic field a stationary point charge. A magnetic field cannot exist without an E field component because there are no magnetic monopoles they are always bi-poles a North Pole and a South Pole and the surface area is always equal to zero.