If 1/0 is infinity and 2/0 is infinity, why isn't 1=2?
- Thread starter Chaman Chopra
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Reeii Education
BANNED
Short answer: 1 times 0 is 0, 2 times 0 is 0 but 1 isn’t 2. It’s the same thing.
For a long answer, take this example:
You have a list of all positive integers. How long would this list be? You’d always go on to the next integer; if you are at 2000 integers, you can increase the amount of integers to 2001, and so on. This list would of course be infinitely long.
Now we’re going to take a list of all positive EVEN integers. Would this list be smaller, longer or just as long as the previous list?
The answer is: it’d be just as long. For example, if you had the numbers from 1 all the way up to 1000 in the first list, you can always use all the EVEN numbers from 2 to 2000 to have a list of the same length. This means that 2 times infinity is the same as one infinity.
Now back to your question. If 1/0 equals infinity, then 2/0 would be the same as 2 times 1/0, which would be the same as 2 times infinity, but 2 times is one, so that’s why 1/0 is infinity, 2/0 is infinity but 1 is not 2.
For a long answer, take this example:
You have a list of all positive integers. How long would this list be? You’d always go on to the next integer; if you are at 2000 integers, you can increase the amount of integers to 2001, and so on. This list would of course be infinitely long.
Now we’re going to take a list of all positive EVEN integers. Would this list be smaller, longer or just as long as the previous list?
The answer is: it’d be just as long. For example, if you had the numbers from 1 all the way up to 1000 in the first list, you can always use all the EVEN numbers from 2 to 2000 to have a list of the same length. This means that 2 times infinity is the same as one infinity.
Now back to your question. If 1/0 equals infinity, then 2/0 would be the same as 2 times 1/0, which would be the same as 2 times infinity, but 2 times is one, so that’s why 1/0 is infinity, 2/0 is infinity but 1 is not 2.
Last edited by a moderator:
Since infinity is unmeasurable, then in comparison 1 & 2 are in a sense unnoticed or rounded to an equal state, therefor equating an equal value which would then generally be normalized as 0. - conceptual mathematics.
Infinity is not a number. It is a concept, as stated much better above me lol.
When you resolve the fractions, you don't get 1 and 2. You get 0 and 0, hence, infinity.
A better way of writing out '2/0' is 'two zeroeths'. What is a ratio of two to zero? there isn't one. this doesnt not equate to a number, it's a concept. the answer doesn't matter.
even easier to express it like this.
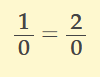
To get rid of the 0s, you have to multiply both sides by the lowest common denominator. That happens to be infinity, or zero. Same thing.
1/0(∞) = 2/0(∞)
1(∞) = 2(∞)
since 2 infinite is equivalent to 1 infinity, (as they are meaningless, you can just express it as
∞ = ∞
alternatively
1/0(0) = 2/0(0)
0 = 0
more strictly, 2/0 = #DIV/0!
When you resolve the fractions, you don't get 1 and 2. You get 0 and 0, hence, infinity.
A better way of writing out '2/0' is 'two zeroeths'. What is a ratio of two to zero? there isn't one. this doesnt not equate to a number, it's a concept. the answer doesn't matter.
even easier to express it like this.
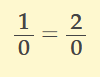
To get rid of the 0s, you have to multiply both sides by the lowest common denominator. That happens to be infinity, or zero. Same thing.
1/0(∞) = 2/0(∞)
1(∞) = 2(∞)
since 2 infinite is equivalent to 1 infinity, (as they are meaningless, you can just express it as
∞ = ∞
alternatively
1/0(0) = 2/0(0)
0 = 0
more strictly, 2/0 = #DIV/0!
But, 2/0=1/0= infinity, out of context, means that both ratios are large without limit, not that 2=1.
When you divide 10 by 2, you get 5, because there are 5 "2's" in 10. When you divide 10 by 0, you get no single numerical result of any use to most of us.
However, if you define 0 as a limit of a series of numbers that get smaller and smaller, then
2/(number in the series) gets bigger and bigger. In mathematical modeling of the physical world, this could mean an instability leading to disaster, or a singularity that is not intuitively related to a physical process.
If the number in the series is the same for both 1/number and 2/number, then, as the numbers in the series get smaller, 2/number will be twice 1/number at each number in the series. E.g.,
Series 1, .5, .25, .125, .0625, ...., approaching as small a number as close to zero as you like
2/number is itself a series: 2, 4, 8, 16, 32 ...., always twice the value at each step
1/number is itself a series: 1, 2, 4, 8, 16 ...,
so, (2/number) = 2 times (1/number), for all values of the number as it gets smaller and smaller.
The use of the word infinity means that there is no end to the increase in size of these ratios.
Disclaimer: Mathematicians will always humble me in this sort of discussion.
When you divide 10 by 2, you get 5, because there are 5 "2's" in 10. When you divide 10 by 0, you get no single numerical result of any use to most of us.
However, if you define 0 as a limit of a series of numbers that get smaller and smaller, then
2/(number in the series) gets bigger and bigger. In mathematical modeling of the physical world, this could mean an instability leading to disaster, or a singularity that is not intuitively related to a physical process.
If the number in the series is the same for both 1/number and 2/number, then, as the numbers in the series get smaller, 2/number will be twice 1/number at each number in the series. E.g.,
Series 1, .5, .25, .125, .0625, ...., approaching as small a number as close to zero as you like
2/number is itself a series: 2, 4, 8, 16, 32 ...., always twice the value at each step
1/number is itself a series: 1, 2, 4, 8, 16 ...,
so, (2/number) = 2 times (1/number), for all values of the number as it gets smaller and smaller.
The use of the word infinity means that there is no end to the increase in size of these ratios.
Disclaimer: Mathematicians will always humble me in this sort of discussion.
They never did, but thats a short answer they give to kids who ask why they can't put it in thier ti-84.When did they start teaching that 1/0 = infinity? New math again?
Thank you for sharing it with us.
Hope you find more math problems like this and keep us posted.
FaceTime Download
Hope you find more math problems like this and keep us posted.
FaceTime Download
I understand division by zero to be undefined; i.e.: call it infinity, call Charlie. Basically, any multiplication by zero is the equivalent of doing nothing i.e.: the product is zero, a place holder on an arithmetic scale.
Similar threads
- Replies
- 2
- Views
- 554
- Replies
- 0
- Views
- 623
- Replies
- 0
- Views
- 352
TRENDING THREADS
-
Ultrafast laser-powered 'magnetic RAM' is on the horizon after new discovery
- Started by admin
- Replies: 0
-
IIT Coaching Institute in Gorakhpur
- Started by academicheightscbse@gmail
- Replies: 0
-
-
-
What is a living individual and is it naturally universally mobile?
- Started by tonylang
- Replies: 138
-
Important Astronomy - No elliptic orbit and relativity break through
- Started by TheBox
- Replies: 63

Live Science is part of Future plc, an international media group and leading digital publisher. Visit our corporate site.
© Future Publishing Limited Quay House, The Ambury, Bath BA1 1UA. All rights reserved. England and Wales company registration number 2008885.
