You must remember Einstein:
E = mc² .
Energy and matter are the same.
Through careful observations of the photoelectric effect, Albert Einstein realized that there were several characteristics that could be explained only if
Electro Magnetic radiation is itself quantized. Einstein’s idea is very important. It means that the apparently continuous stream of energy in an EM wave is actually not a continuous stream at all. In fact, the EM wave itself is actually composed of tiny quantum packets of energy called photons.
In equation form, Einstein found the energy of a photon or photoelectron to be
𝐸=ℎf,E=hf,
where
E is the energy of a photon of frequency
f and
h is Planck’s constant. A beam from a flashlight, which to this point had been considered a wave, instead could now be viewed as a series of photons, each providing a specific amount of energy. Furthermore, the amount of energy within each individual photon is based upon its individual frequency, as dictated by 𝐸=ℎ𝑓.E=hf. As a result, the total amount of energy provided by the beam could now be viewed as the sum of all frequency-dependent photon energies added together.
E = mc² states that energy is equal to an object’s mass multiplied by the speed of light squared. This simple-seeming mathematical relation holds an enormous amount of physics inside of it, including:
- if you have a certain amount of energy available, you can spontaneously create new matter-antimatter pairs of particles as long as their rest mass is less than the amount of energy required to create them,
- if a matter-antimatter pair of particles annihilates, they will produce a specific amount of energy given by the masses of the pair of particles that annihilated,
- and that every time you have a nuclear reaction, whether fusion or fission, if the mass of the products is less than the mass of the reactants, E = mc² tells you how much energy will be liberated in that reaction.
This one equation,
E = mc², describes how much energy is inherent to any massive particle at rest, including how much energy it takes to create it and how much energy is released if you destroy it.
But what if your particle isn’t at rest, or what if it doesn’t have any mass at all? In those cases,
E = mc² is only half of the meaningful equation. The other half is far more interesting, and is required to make physical sense of what’s going on.
The reason “rest mass” is such an important concept is because motion — the rate of change of an object’s position over time — isn’t an “absolute” physical property in our Universe. Instead, the key lesson from Einstein’s relativity is that irrespective of what your position is or how your position is changing with time, the laws of physics and the constants of nature, including the speed of light, are always going to appear to be the same.
When you’re in motion, your energy isn’t just given by your rest-mass energy, which is the
mc² contribution to your energy. Instead, you also have kinetic energy: the energy of motion itself.
Whenever two objects collide, whether they stick together (inelastically) or bounce off of one another (elastically), it’s the kinetic energy that they possess, based on their motion relative to one another, that determines how fast they’ll each wind up moving after they crash into each other. This “energy of motion,” or kinetic energy, is essential to the physics of objects in motion, from billiard balls to automobiles to planetary systems.
A quantum of energy that has no rest mass at all. Light, whether we treat it as a wave whose energy is defined by its wavelength or a particle whose energy is quantized into packets known as photons, has no rest mass, so the
m in
E = mc² has to equal zero. But light carries energy, so
E = mc²can’t be all that there is, or
E would equal zero, too, which it cannot.
There’s a hint toward the solution when you learned about the “standard” formula for kinetic energy:
KE = ½mv², where
v is the speed of the object in motion. This formula only applies at speeds that are low compared to the speed of light: where
v is much smaller than
c, the speed of light in a vacuum. (That’s the same “
c” that’s in
E = mc²: 299,792,458 m/s.)
The reason that “kinetic energy” offers such a useful hint is because it leads you one step closer to the real key concept in completing Einstein’s most famous equation: momentum.
Momentum is the “quantity of motion” that an object has, and it’s well-defined whether the thing that’s in motion is massive or massless, and, if massive, whether it moves close to the speed of light or not. Momentum, labeled with a
p for very Latin reasons — arising either from the verb “pellere” (to push forcefully) or “petere” (to go) — is basically a measure of how much “Ooomph!” an object has to its motion, and consequently, how difficult it is to bring it to rest.
- For massive particles moving slow compared to the speed of light, momentum can be well-approximated by the simple formula p = mv.
- For massive particles moving at any speed, even at a substantial fraction of the speed of light, momentum is more precisely written p = mγv, where “γ” is the Lorentz factor: 1/√(1-(v/c)²).
- And for massless particles, like light, that move at the speed of light and have no rest mass at all, momentum can’t be written in terms of mass, but can be written in terms of energy very simply, as p = E/c.
If we want to give the true expression for the energy inherent to any particle, then, we need to include the effects of its quantity of motion on energy as well as its rest mass’s effects on energy.
E = mc², as simple, compact, and notorious as it is, only applies to massive particles at rest: a useful quantity only in certain cases.
Fortunately, there’s an almost-as-simple formula that incorporates both the rest mass energy of a particle, when present, along with the contribution of its quantity of motion to energy as well. That formula for energy is as follows:
E = √(
m²c⁴ +
p²c²)
Think about what happens in all the different cases that apply here. If momentum (
p) is zero, then that last term goes away entirely, and you simply get
E = √(
m²c⁴), which just becomes good old
E = mc² once again: Einstein’s original rest mass-energy equivalence equation.
What if we’re moving slow compared to the speed of light, and we just put in
p = mv for momentum?
Then the equation becomes
E = √(
m²c⁴ +
m²v²c²), or, if we pull out an
mc² from inside the square root,
E = mc² *
√(1 + (
v/
c)
²).
This might not look particularly familiar, but consider the following: this equation only works for values of speed, or
v, that are slow compared to the speed of light, or
c in this equation.
Therefore, the part of the equation that reads
√(1 + (
v/
c)
²) is only going to be a little bit greater than one, because the (
v/
c) term is small. Whenever you have, in mathematics, an expression that’s
√(1 + x), wherever “x” is small compared to 1, it can be excellently approximated by 1 + ½*x.
If we do that to our expression for energy, we turn
√(1 + (
v/
c)
²) into 1 + ½*(
v/
c)
², which turns our expression for energy into
E = mc² * (1 + ½*(
v/
c)
²),
which becomes, when we multiply the terms out:
E = mc² + ½
mv²,
which tells us that the total energy is the rest mass energy (the
mc² part) plus the kinetic energy (the ½
mv² part).
When considering a massive particle moving close to the speed of light, however, we can no longer make any such approximations with any sort of reliability; you simply have to calculate the full thing for yourself, using the equation
E = √(
m²c⁴ +
p²c²).
But as you get to very high momentums, which is precisely the case that we deal with in our largest and most powerful particle accelerators, the rest mass term contributes very little to the overall energy. At 99.999%+ the speed of light, the
m²c⁴ term will be much smaller than the
p²c² term in the equation, which means we can neglect it.
If we do, then we simply get
E = √(
p²c²), which becomes
E = pc: the equation for the energy-momentum relationship for photons and other massless particles. We sometimes call this the ultra-relativistic approximation, as it’s useful wherever the rest mass energy of a system is small compared to the energy due to motion; we can neglect that first term — the
m²c⁴ term — even if the object moving ultra-relativistically isn’t truly massless.
According to Einstein’s theory, the presence of a large amount of energy, all in one location in spacetime (the Sun), would bend and distort the path of all objects that traveled close to it. This included the light from background stars, which, although massless, would still follow the path created by curved space: the important key concept of General Relativity.
But what would the older theory that General Relativity was trying to supersede — Newton’s theory of universal gravitation — predict?
Some people insisted that Newton would predict zero deflection, since light particles, or photons, had no rest mass and Newton’s theory relied solely on mass for gravitational attraction. But others recognized that photons still carried energy in the form of
E = pc, and therefore, if you used the energy that photons had in place of where you would’ve typically used mass (i.e., if you substituted a photon’s
E/
c² in place of the Newtonian mass,
m), you could actually predict a deflection for Newtonian gravity, too. The fact that Einstein’s theory predicted double the Newtonian value, and that was indeed borne out by the observations, was the key test that enabled us to verify and validate Einstein’s theory, leading to a revolution in how we understood the Universe.
You should still recognize how profound the simple statement,
E = mc², actually is. It tells us that every massive particle has an inherent amount of energy inherent to it, even when it’s at rest, and that its energy can never drop below that key value:
mc². If you want to create a particle like it, you require at least that much energy; if you must create that particle along with its antiparticle counterpart, you require at least double that energy. And if you destroy or annihilate any massive particle away, all of that rest mass energy, all
mc² of it, will become part of the energy that all of the “daughter particles,” or particles produced in the annihilation, carry away.
But you should also recognize that
E = mc² is only part of the full story: because particles not only exist at rest, but also move through the Universe. The quantity of motion that they carry with them, momentum, leads to a certain amount of energy-of-motion being associated with that particle as well. For slow-moving, massive particles, you can approximate that energy-of-motion with
E = ½mv². For massless particles and ultra-relativistic massive particles, you can approximate that energy of motion with
E = pc. But if you want the general case, where rest mass and momentum both are included, you need the full equation for the energy of a particle:
E = √(
m²c⁴ +
p²c²)
As famous as it is,
E = mc² is only half of the full equation that’s needed to describe a particle’s energy. To get the other half, you have to remember that you cannot simply describe the Universe by taking a snapshot of it. It has a kind of beauty — and energy — that is moving.
Hartmann352
See:
https://chem.libretexts.org/Courses...tric_Effect_Explained_with_Quantum_Hypothesis
See:
https://link.springer.com/article/10.1007/s10773-022-05154-2
See:
https://bigthink.com/starts-with-a-bang/einsteins-e-mc-squared-half-equation/
The intensity of radiation is a measure of the energy emitted per unit area. A plot of the intensity of blackbody radiation as a function of wavelength for an object at various temperatures is shown in Figure 2. One of the major assumptions of classical physics was that energy increased or decreased in a smooth, continuous manner. For example, classical physics predicted that as wavelength decreased, the intensity of the radiation an object emits should increase in a smooth curve without limit at all temperatures, as shown by the broken line for 6000 K in Figure 2. Thus classical physics could not explain the sharp decrease in the intensity of radiation emitted at shorter wavelengths (primarily in the ultraviolet region of the spectrum), which was referred to as the “ultraviolet catastrophe.” In 1900, however, the German physicist Max Planck (1858–1947) explained the ultraviolet catastrophe by proposing (in what he called "an act of despair") that the energy of electromagnetic waves is quantized rather than continuous. This means that for each temperature, there is a maximum intensity of radiation that is emitted in a blackbody object, corresponding to the peaks in Figure 2, so the intensity does not follow a smooth curve as the temperature increases, as predicted by classical physics.
Thus energy could be gained or lost only in integral multiples of some smallest unit of energy, a quantum.
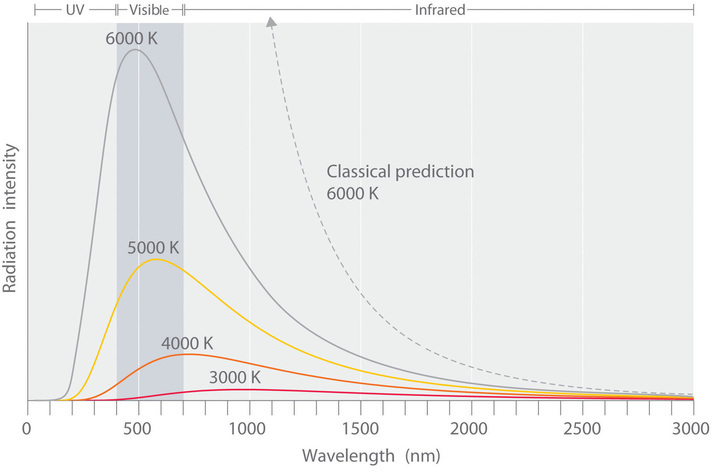
Figure 2 Relationship between the Temperature of an Object and the Spectrum of Blackbody Radiation it emits. At relatively low temperatures, most radiation is emitted at wavelengths longer than 700 nm, which is in the infrared portion of the spectrum. The dull red glow of the electric stove element is due to the small amount of radiation emitted at wavelengths less than 700 nm, which the eye can detect. As the temperature of the object increases, the maximum intensity shifts to shorter wavelengths, successively resulting in orange, yellow, and finally white light. At high temperatures, all wavelengths of visible light are emitted with approximately equal intensities. The white light spectrum shown for an object at 6000 K closely approximates the spectrum of light emitted by the sun. Note the sharp decrease in the intensity of radiation emitted at wavelengths below 400 nm, which constituted the ultraviolet catastrophe. The classical prediction fails to fit the experimental curves entirely and does not have a maximum intensity.
When heated, all objects emit electromagnetic radiation whose wavelength (and color) depends on the temperature of the object. A relatively low-temperature object, such as a horseshoe forged by a blacksmith, appears red, whereas a higher-temperature object, such as the surface of the sun, appears yellow or white.
See:
https://chem.libretexts.org/Courses...zation:_Planck,_Einstein,_Energy,_and_Photons

